前言
重拾$AtCoder$,还是一样的自闭。
现在还是非常欠缺思维?特别是这种代码很轻量但总是找不到入手点的题目。
题目大意
给定两个数$B,C$,有如下两种操作:
- $C - 1: \quad B * (-1)$
- $C - 2: \quad B - 1$
每次操作完后,$B$变为操作后得到的那个数。
其中,$C$必须始终满足$C \geq 0$,求能够通过这两种操作能够得到的$B$有多少个。
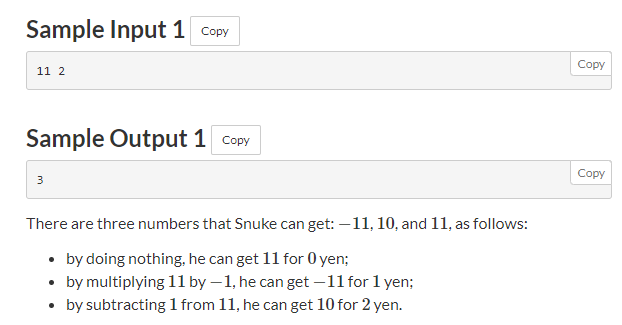
样例解释如下:
思路
开始的时候,一直在考虑构造一种最优的方法,来尽可能达到更多的数。
但其实没有这个必要,因为题目要求的是能够到达多少个数,也就是说,只要存在一种方法能够到达就行了。
后面继续考虑,按照每次都是减$1$,然后$ (-1)$的顺序进行构造,考虑能够到达的边界。后发现有的时候是先$ (-1)$,再减$1$,这样才会更优。于是这个想法就先被搁置了。
这个想法到最后都没有实现,后面看评论区,发现每种操作都模拟一次,就可以了。

后面队友发挥了奇妙的数学能力,利用尽可能拓展的思想,推出来两个区间,只需要求出两区间并集的元素个数就行。这个时候已经非常接近正解,不过队友的区间式子比较奇怪,只能过八个点,后面很多点都$WA$了。
队友考虑:
$B\geq0$时的式子
$B < 0$时的式子
变为代码后:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| #include <bits/stdc++.h>
#define int long long
using namespace std;
signed main(void)
{
int B, C, ans;
scanf("%lld %lld", &B, &C);
if(B >= 0)
{
int l1 = - B - (C - 1) / 2;
int r1 = - B;
int l2 = B - C / 2;
int r2 = B + (C - 2) / 2;
if(r1 < l2)
ans = r1 - l1 + 1 + r2 - l2 + 1;
else if(r1 >= l2 && l2 >= l1)
ans = r1 - l1 + 1 + r2 - l2 + 1 - (r1 - l2 + 1);
else
ans = r2 - l2 + 1;
}
else
{
int l1 = B - C / 2;
int r1 = B;
int l2 = - B - (C - 1) / 2;
int r2 = - B + (C - 2) / 2;
if(r1 < l2)
ans = r1 - l1 + 1 + r2 - l2 + 1;
else if(r1 >= l2 && l2 >= l1)
ans = r1 - l1 + 1 + r2 - l2 + 1 - (r1 - l2 + 1);
else
ans = r2 - l2 + 1;
}
printf("%lld\n", ans);
return 0;
}
|
这样的式子能过所有的样例,但过不了所有数据。
后来,我的队友”表王”利用暴力打表,推出了一个分类讨论规律的程序,并成功$AC$。
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| #include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll b, c;
int main()
{
cin >> b >> c;
if (b == 0)
cout << c << endl;
else if (c == 1)
cout << 2 << endl;
else if (b > 0 && b <= c / 2)
cout << b + c + b - 1 << endl;
else if (b > 0 && b > c / 2 && (c & 1))
cout << c / 2 + c / 2 + c << endl;
else if (b > 0 && b > c / 2 && (c % 2 == 0))
cout << 2 * c - 1 << endl;
else if (b < 0 && llabs(b) <= c / 2 && (c & 1))
cout << llabs(b) + llabs(b - 1) + c << endl;
else if (b < 0 && llabs(b) > c / 2 && (c & 1))
cout << 2 * c + 1 << endl;
else if (b < 0 && llabs(b) <= c / 2 && (c % 2 == 0))
cout << llabs(b) * 2 + c << endl;
else if (b < 0 && llabs(b) > c / 2 && (c % 2 == 0))
cout << 2 * c << endl;
return 0;
}
|
再后来,学习官方正解,总结如下。
假设$C-2$的能够到达某些数,那么$C$也一定能够达到那些数。
也就是说,最后我们只需要计算消耗恰好为$C$和$C-1$两种情况,就能解决问题。
另外,分为$C$为奇数和偶数进行讨论:
当$C$为奇数时,可以表示为$C=2n+1$,此时贪心的想,假设全部相减,并在某一次乘上$-1$,则得到左边界为$-B-n$,右边界为$-B+n$。
举例如下:
同理,在$C$为偶数时,分两种情况:
- 全部的$C$用于相减,即左边界为$B-n$;
- 相乘一次$-1$,余下的$C$用于相减(相当于在初始的$B$上相加)
可以分别得到左边界$B-n$,右边界$B+n-1$。
特别的,当$C$为$0$时,什么操作都不需要做,左右边界均为$B$。
综合这两种情况,并计算$C$和$C-1$情况下的并集,就可以解决该题。
同时也学习了一个快速求区间并的做法,记录:
转化为代码,得:
(参照官方,写的返回$pair$,代表左右区间)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| #include <bits/stdc++.h>
#define int long long
using namespace std;
int B, C;
pair<int, int> calc(int C){
if(C & 1){
return make_pair(- B - C / 2, - B + C / 2);
}
else{
if(C == 0)
return make_pair(B, B);
return make_pair(B - C / 2, B + C / 2 - 1);
}
}
signed main(void)
{
scanf("%lld %lld", &B, &C);
int l1, r1, l2, r2, n;
pair<int, int> res;
res = calc(C);
l1 = res.first, r1 = res.second;
res = calc(C - 1);
l2 = res.first, r2 = res.second;
printf("%lld\n", r1 - l1 + 1 + r2 - l2 + 1 - max(0LL, min(r1, r2) - max(l1, l2) + 1));
return 0;
}
|
over
该题的做法好像很多,评论区里也有别的求并集的方法:

要是现场遇到这题,那真的是铁铁了…


