题意

给定一个序列$[a_i]$，求这个序列的所有子串$[i…j]$中，满足$a_k=a_l$的对数的和，其中$i \leq k < l \leq j$。

或（图源 Zhihu@Forward Star）：

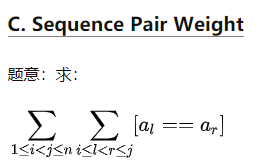
image-20210521171317062

思路

最开始拿到这题的时候，感觉上应该是一种计数题，需要统计每一对的贡献，或者每一位的贡献，最后加在一起。

于是提出第一个思路，假设必选$a_i$，那么贡献有多少？

必选$a_i$，则可以与$a_i$左边的与$a_i$相同的数字配对，与$a_i$右边的也是一样。

假设右边有$k$个与$a_i$相同的数，则：

假定只选前两个，则选择的对数为$C^2_2$；

选择前三个，即$a_i, g_1, g_2$，则选择的对数为$C^2_3$；

$a_i$和$[g]$这些，都可以通过$map$来辅助记录。

由此，可以维护一个前缀和，$\sum C^2_i$，来解决i为左端点，g对应的位置一定是右端点的情况下的计数。

但是，本题要求所有子串的贡献。于是，我又考虑加上对与$a_i$不同的元素的支持$diff$。

不过，很快发现，加上了$diff$作为贡献后，与前缀和的性质发生了冲突，不能够快速求解了。

然后，比赛就结束了（

赛后研究题解，才发现自己想的确实复杂了。

对于任一对数$(a_i, a_j)$，子串的选择方法有$i (n - j + 1)$中，其中，$i$可以理解成左端点的选择方案数，$n-j+1$可以理解成右端点的选择方案数，合起来就是当前这一对数$(a_i,a_j)$能够在$i(n-j+1)$个子串中做出贡献。

那么，假设当前枚举到了$a_i$，前面有两个与$a_i$相同的数$a_j,a_k$怎么办呢？

如果是一个个枚举，那么复杂度是$O(n^2)$的，无法通过此题。

我们可以利用$map$，规定一个方向，然后，每遇到一个数字时，就把对应的选择可能方案数加到$map$里面。

以上面那个为例，假设$j < k$

  1. 遍历到$a_j$，前面没有相同的元素，直接$mp[a_j] = mp[a_j] + j$

  2. 遍历到$a_k$，前面有一个相同的元素$a_j$，得到$ans = ans + mp[a_j] * (n - k + 1)$。更新完答案后再更新$mp$。

  3. 遍历到$a_i$，前面有两个相同的元素$a_j, a_k$。

    此时$mp[a_i]=(j + k)$，拆分开也就是$j (n - i + 1) + k (n - i + 1)$，即一起计算了$(a_j, a_i)$和$(a_k, a_i)$的贡献。由此更新答案，更新完答案后再更新$mp$。

其他情况以此类推，只需要$O(nlogn)$就可以解决。

$O(logn)$主要是$map$的复杂度，如果使用$unordered \ map$可以做到$O(n)$。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <bits/stdc++.h>
#define maxn 1000005
#define int long long
using namespace std;
int t, n, a[maxn];
signed main(void)
{
    scanf("%lld", &t);
    while(t--)
    {
        int ans = 0;
        map<int, int> cnt;
        scanf("%lld", &n);
        for(int i = 1; i <= n; i++)
        {
            scanf("%lld", &a[i]);
            if(cnt.count(a[i]))    ans += cnt[a[i]] * (n - i + 1);
            cnt[a[i]] += i;
        }
        printf("%lld\n", ans);
    }
    return 0;
}

别的

（刚铁完回来，本来还想发发游记来着，不过也没什么好发的了）

继续训练。