背景
不多的我院人人皆知竞赛?
入门难度相对较小,但是说实话,要拿奖也绝非易事。
第一年报个$B$组试试水,希望不要省赛就白给掉了,然后在国赛要是能摸个国二就最好了。
然后感谢罗勇军老师$CSDN$博客里面的每日一题,目前还是跟着在做!
以及感谢$New Online Judge$提供评测!
题目
基本上就是一个$DFS$+模拟。
不过题目给出的数据很小,实际上用手数也能数出来,但是为了确认正确性还是写一下代码比较好。
这类代码要快狠准,不能拖沓浪费了后面的时间。
为了方便读入,简单按照快读的模板写了个过滤用的字符读入函数。
然后,开始$DFS$,利用vis数组判断是否已经达到过,can数组判断是否能够离开迷宫。
顺着对每一个vis为$0$的点都作为起点进行一遍$DFS$,最后统计can[i][j]==1的数目即可。
(上面can数组中,不可达我定义为$-1$)
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
| #include <bits/stdc++.h>
#define maxn 105
using namespace std;
int vis[maxn][maxn], can[maxn][maxn];
char board[maxn][maxn];
char read(){
char ch = getchar();
while(ch < 'A' || ch > 'Z') ch = getchar();
return ch;
}
int dfs(int x, int y){
if(x < 1 || x > 10 || y < 1 || y > 10)
return can[x][y] = 1;
if(vis[x][y])
return can[x][y] = (can[x][y] == 1 ? 1 : -1);
vis[x][y] = 1;
if(board[x][y] == 'U')
can[x][y] = dfs(x - 1, y);
if(board[x][y] == 'D')
can[x][y] = dfs(x + 1, y);
if(board[x][y] == 'L')
can[x][y] = dfs(x, y - 1);
if(board[x][y] == 'R')
can[x][y] = dfs(x, y + 1);
return can[x][y];
}
int main(void)
{
for(int i = 1; i <= 10; i++)
for(int j = 1; j <= 10; j++)
board[i][j] = read();
for(int i = 1; i <= 10; i++)
for(int j = 1; j <= 10; j++)
if(!vis[i][j]) dfs(i, j);
int ans = 0;
for(int i = 1; i <= 10; i++)
for(int j = 1; j <= 10; j++)
if(can[i][j] == 1) ans++;
printf("%d\n", ans);
return 0;
}
|
标准搜索题。
和八数码问题,魔板问题啥的差不多,主要就是设计一个状态,然后进行$BFS$。
状态我更喜欢用字符串来表示,这样用$set$判重也很方便!
我是利用"123456780", "876543210"这两个字符串来表示起始状态和结束状态,剩下的就是编写如何转移了。
容易发现,每次转移的情况都只有$4$种:
- 空盘左边一位的蚱蜢跳进去
- 空盘右边一位的蚱蜢跳进去
- 空盘左边两位的蚱蜢跨过左边一位的蚱蜢跳进去
- 空盘右边两位的蚱蜢跨过右边一位的蚱蜢跳进去
这样的过程用$swap$交换一下即可。
为了获取最小步数,我常使用结构体打包当前状态和当前步数,方便快捷。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
| #include <bits/stdc++.h>
#define maxn 100005
using namespace std;
set<string> used;
struct Status{
int step;
string sta;
};
int calc(int x){
return (x + 9) % 9;
}
int bfs(string s, string t){
queue<Status> q1;
q1.push((Status){0, s});
used.insert(s);
while(!q1.empty())
{
Status now = q1.front();
q1.pop();
if(now.sta == t) return now.step;
int pos = -1;
for(int i = 0; i <= now.sta.length() - 1; i++)
if(now.sta[i] == '0')
{
pos = i;
break;
}
swap(now.sta[calc(pos - 1)], now.sta[pos]);
if(!used.count(now.sta))
{
used.insert(now.sta);
q1.push((Status){now.step + 1, now.sta});
}
swap(now.sta[calc(pos - 1)], now.sta[pos]);
swap(now.sta[calc(pos + 1)], now.sta[pos]);
if(!used.count(now.sta))
{
used.insert(now.sta);
q1.push((Status){now.step + 1, now.sta});
}
swap(now.sta[calc(pos + 1)], now.sta[pos]);
swap(now.sta[calc(pos - 2)], now.sta[pos]);
if(!used.count(now.sta))
{
used.insert(now.sta);
q1.push((Status){now.step + 1, now.sta});
}
swap(now.sta[calc(pos - 2)], now.sta[pos]);
swap(now.sta[calc(pos + 2)], now.sta[pos]);
if(!used.count(now.sta))
{
used.insert(now.sta);
q1.push((Status){now.step + 1, now.sta});
}
swap(now.sta[calc(pos + 2)], now.sta[pos]);
}
}
int main(void)
{
printf("%d\n", 20);
return 0;
}
|
这是一道我考场上打死都不去碰的题。
(除非我对于这道题的数学解法比较熟悉并且能够快速解出来)
因为这个魔方本质不同的情况实在是很难设计出状态完全表示出来。
我的做法是模拟魔方的滚动(上下滚动,左右滚动),然后观察滚动的每一种状态是否有出现过。
为了更方便的模拟滚动,我直接写了个简单的$DFS$,在七步之内,遍历每种上下,左右的滚动方案,保证能够找出所有本质相同的方案。
剩下的部分其实就是暴力模拟搜索了,只要模仿魔方的拧动不断$BFS$即可。
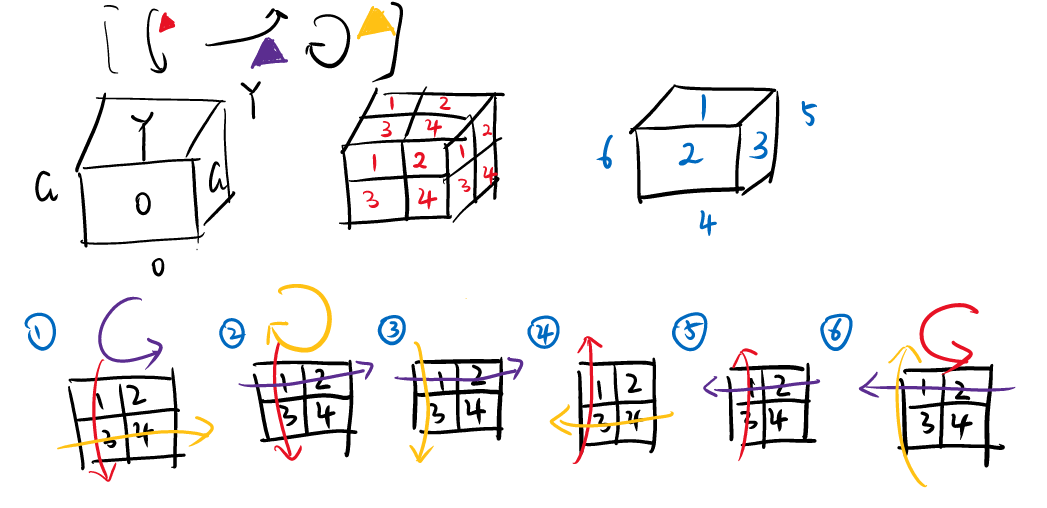
(也只有在非考试状态下才会慢慢写个大搜索来调试)
事实证明并不是前面的题就简单的,还是应该先把能骗得拿到手,剩下的随缘。
这题网上的代码也有一份大模拟流传,不过据说要跑$20min$?
我这份代码相对要更快一些,大概$5s$内就出结果了。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
| #include <bits/stdc++.h>
#define maxn 100005
using namespace std;
int ans;
set<string> s1;
queue<string> q1;
string updown(string s){
string tmp = s;
s[1] = tmp[3 + 4 * 4]; s[2] = tmp[4 + 4 * 4];
s[3] = tmp[1 + 4 * 4]; s[4] = tmp[2 + 4 * 4];
s[1 + 4] = tmp[1]; s[2 + 4] = tmp[2];
s[3 + 4] = tmp[3]; s[4 + 4] = tmp[4];
s[1 + 4 * 3] = tmp[3 + 4]; s[2 + 4 * 3] = tmp[4 + 4];
s[3 + 4 * 3] = tmp[1 + 4]; s[4 + 4 * 3] = tmp[2 + 4];
s[1 + 4 * 4] = tmp[1 + 4 * 3]; s[2 + 4 * 4] = tmp[2 + 4 * 3];
s[3 + 4 * 4] = tmp[3 + 4 * 3]; s[4 + 4 * 4] = tmp[4 + 4 * 3];
s[1 + 4 * 2] = tmp[2 + 4 * 2];
s[2 + 4 * 2] = tmp[4 + 4 * 2];
s[3 + 4 * 2] = tmp[1 + 4 * 2];
s[4 + 4 * 2] = tmp[3 + 4 * 2];
s[1 + 4 * 5] = tmp[2 + 4 * 5];
s[2 + 4 * 5] = tmp[4 + 4 * 5];
s[3 + 4 * 5] = tmp[1 + 4 * 5];
s[4 + 4 * 5] = tmp[3 + 4 * 5];
return s;
}
string leftright(string s){
string tmp = s;
s[1 + 4 * 1] = tmp[2 + 4 * 5]; s[2 + 4 * 1] = tmp[1 + 4 * 5];
s[3 + 4 * 1] = tmp[4 + 4 * 5]; s[4 + 4 * 1] = tmp[3 + 4 * 5];
s[1 + 4 * 2] = tmp[1 + 4 * 1]; s[2 + 4 * 2] = tmp[2 + 4 * 1];
s[3 + 4 * 2] = tmp[3 + 4 * 1]; s[4 + 4 * 2] = tmp[4 + 4 * 1];
s[1 + 4 * 4] = tmp[2 + 4 * 2]; s[2 + 4 * 4] = tmp[1 + 4 * 2];
s[3 + 4 * 4] = tmp[4 + 4 * 2]; s[4 + 4 * 4] = tmp[3 + 4 * 2];
s[1 + 4 * 5] = tmp[1 + 4 * 4]; s[2 + 4 * 5] = tmp[2 + 4 * 4];
s[3 + 4 * 5] = tmp[3 + 4 * 4]; s[4 + 4 * 5] = tmp[4 + 4 * 4];
s[1 + 4 * 0] = tmp[2 + 4 * 0];
s[2 + 4 * 0] = tmp[4 + 4 * 0];
s[3 + 4 * 0] = tmp[1 + 4 * 0];
s[4 + 4 * 0] = tmp[3 + 4 * 0];
s[1 + 4 * 3] = tmp[2 + 4 * 3];
s[2 + 4 * 3] = tmp[4 + 4 * 3];
s[3 + 4 * 3] = tmp[1 + 4 * 3];
s[4 + 4 * 3] = tmp[3 + 4 * 3];
return s;
}
bool dfs(string now, int cnt){
if(cnt == 7)
return !s1.count(now);
bool flag = !s1.count(now);
flag &= dfs(updown(now), cnt + 1);
flag &= dfs(leftright(now), cnt + 1);
return flag;
}
bool check(string now){
return dfs(now, 0);
}
string change1(string s){
string tmp = s;
s[1] = tmp[3 + 4 * 4];
s[3] = tmp[1 + 4 * 4];
s[1 + 4] = tmp[1];
s[3 + 4] = tmp[3];
s[1 + 4 * 3] = tmp[3 + 4];
s[3 + 4 * 3] = tmp[1 + 4];
s[1 + 4 * 4] = tmp[1 + 4 * 3];
s[3 + 4 * 4] = tmp[3 + 4 * 3];
s[1 + 4 * 5] = tmp[2 + 4 * 5];
s[3 + 4 * 5] = tmp[1 + 4 * 5];
s[4 + 4 * 5] = tmp[3 + 4 * 5];
s[2 + 4 * 5] = tmp[4 + 4 * 5];
return s;
}
string change2(string s){
string tmp = s;
s[1 + 4 * 1] = tmp[2 + 4 * 5];
s[2 + 4 * 1] = tmp[1 + 4 * 5];
s[1 + 4 * 2] = tmp[1 + 4 * 1];
s[2 + 4 * 2] = tmp[2 + 4 * 1];
s[1 + 4 * 4] = tmp[2 + 4 * 2];
s[2 + 4 * 4] = tmp[1 + 4 * 2];
s[1 + 4 * 5] = tmp[1 + 4 * 4];
s[2 + 4 * 5] = tmp[2 + 4 * 4];
s[1] = tmp[2];
s[3] = tmp[1];
s[4] = tmp[3];
s[2] = tmp[4];
return s;
}
string change3(string s){
string tmp = s;
s[3] = tmp[3 + 4 * 5];
s[4] = tmp[1 + 4 * 5];
s[1 + 4 * 2] = tmp[3];
s[3 + 4 * 2] = tmp[4];
s[3 + 4 * 3] = tmp[3 + 4 * 2];
s[4 + 4 * 3] = tmp[1 + 4 * 2];
s[1 + 4 * 5] = tmp[3 + 4 * 3];
s[3 + 4 * 5] = tmp[4 + 4 * 3];
s[1 + 4] = tmp[3 + 4];
s[2 + 4] = tmp[1 + 4];
s[3 + 4] = tmp[4 + 4];
s[4 + 4] = tmp[2 + 4];
return s;
}
void bfs(){
string sta = "#YYYYOOOOGGGGOOOOYYYYGGGG";
q1.push(sta); s1.insert(sta);
while (!q1.empty())
{
string now = q1.front(); q1.pop();
ans++;
string tmp;
tmp = change1(now);
if(!s1.count(tmp) && check(tmp))
s1.insert(tmp), q1.push(tmp);
tmp = change2(now);
if(!s1.count(tmp) && check(tmp))
s1.insert(tmp), q1.push(tmp);
tmp = change3(now);
if(!s1.count(tmp) && check(tmp))
s1.insert(tmp), q1.push(tmp);
if(ans % 10000 == 0)
printf("%d\n", ans);
}
}
int main(void)
{
bfs();
printf("%d\n", ans);
return 0;
}
|
当然这并不是考场上的最优解,这道题的正确打开方法应该是利用群论知识中的伯恩斯坦定理来快速计算。
【学会了就更,todo】
方格分割
一开始走入了染格子颜色的误区。
忘记了一般情况下的搜索都是一笔画的。
因此,如果按照平时的搜索模板,直接去搜索染色格子,搜出来的方案数目会大大减少。
如果是特殊情况,对当前状态下每一染色格子都出发尝试,时间复杂度上面就会差很多。
因此,这题应该考虑更优的情况——对剪的路径进行搜索。
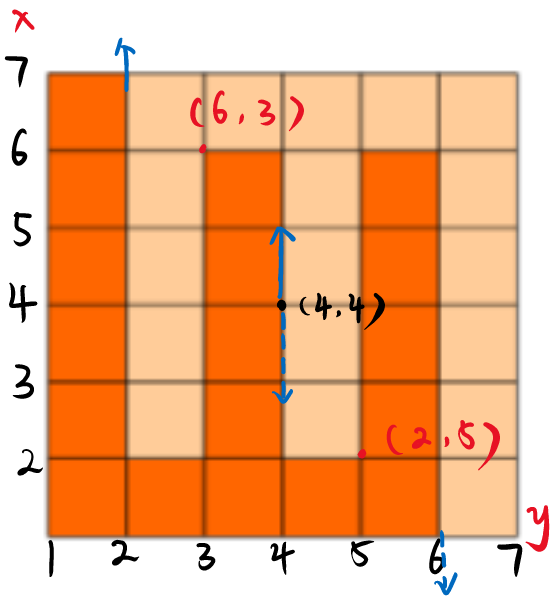
我们对图形建模如上,可以发现,如果按照剪裁的路径搜索,一定会经过点$(4,4)$。
然后,我们搜索半边路径,另外半边路径,根据对称性进行标记。
最后,如果搜索的这半边路径能够顺利剪出,则另外半边也一定能,且剪出来的图形一定对称。
统计答案时,如果不设计旋转判重(类似上一题魔方的判重)的函数,就要推理一下最后的答案与搜出来的方案数的关系。不难发现,由于从中间点出发,每种方案都可以往上,下,左,右进行裁剪。因此,最终答案就是搜索得方案数/4。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| #include <bits/stdc++.h>
#define maxn 1005
using namespace std;
int fx[] = {0, 1, -1, 0, 0};
int fy[] = {0, 0, 0, 1, -1};
int ans, vis[maxn][maxn];
void dfs(int x, int y){
if(x == 1 || y == 1 || x == 7 || y == 7)
{
ans++;
return;
}
for(int i = 1; i <= 4; i++)
{
int nx = x + fx[i], ny = y + fy[i];
if(!vis[nx][ny] && !vis[8 - nx][8 - ny])
{
vis[nx][ny] = 1;
vis[8 - nx][8 - ny] = 1;
dfs(nx, ny);
vis[nx][ny] = 0;
vis[8 - nx][8 - ny] = 0;
}
}
}
int main(void)
{
vis[4][4] = 1;
dfs(4, 4);
printf("%d\n", ans / 4);
return 0;
}
|
字母组串
入门$DP$题,基本没有什么难度。
与HDU1521非常相似,重温了一下指数型生成函数的板子。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
#include <bits/stdc++.h>
#define maxn 1005
using namespace std;
int n, m, num[maxn];
double c1[maxn], c2[maxn];
int func(int x){
if(x == 1 || x == 0)
return 1;
return x * func(x - 1);
}
int main(void)
{
while(~scanf("%d %d", &n, &m))
{
memset(c1, 0, sizeof(c1));
memset(c2, 0, sizeof(c2));
for(int i = 1; i <= n; i++)
scanf("%d", &num[i]);
for(int i = 0; i <= num[1]; i++)
c1[i] = 1.0 / func(i), c2[i] = 0;
for(int i = 2; i <= n; i++)
{
for(int j = 0; j <= num[i]; j++)
for(int k = 0; k + j <= m; k++)
c2[k + j] += c1[k] * 1.0 / func(j);
for(int j = 0; j <= m; j++)
c1[j] = c2[j], c2[j] = 0;
}
printf("%.0lf\n", c1[m] * func(m));
}
return 0;
}
|
最大公共子串
差点写了最大公共子序列的方程上去,好在手推了一下,串是一定要连续的!
总的来说这题难度不大。
快速写了一发交去LeetCode,通过!
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
#include <bits/stdc++.h>
#define maxn 1005
using namespace std;
int ans, dp[maxn][maxn];
string str1, str2;
int main(void)
{
cin >> str1 >> str2;
int len1 = str1.length();
int len2 = str2.length();
for(int i = 0; i <= len1 - 1; i++)
for(int j = 0; j <= len2 - 1; j++)
{
if(str1[i] == str2[j])
{
if(i == 0 || j == 0)
dp[i][j] = 1;
else
dp[i][j] = dp[i - 1][j - 1] + 1;
ans = max(ans, dp[i][j]);
}
}
printf("%d\n", ans);
return 0;
}
|
然后跟着罗老师下面的博客链接,进去重新练了一下入门的$DP$类型,对于编辑距离的问题还有点吃力啊!
要把具体的插入,删除,替换对应到相关方程里面,确实还是有点抽象的。
看来有些经典的$DP$推起来对我还是有点困难的。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
#include <bits/stdc++.h>
#define maxn 1005
using namespace std;
int dp[maxn][maxn];
string word1, word2;
int main(void)
{
cin >> word1 >> word2;
int len1 = word1.length();
int len2 = word2.length();
for(int i = 0; i <= len1; i++)
for(int j = 0; j <= len2; j++)
{
if(i == 0) dp[0][j] = j;
else if(j == 0) dp[i][0] = i;
else
{
if(word1[i - 1] == word2[j - 1])
dp[i][j] = dp[i - 1][j - 1];
else
dp[i][j] = min(dp[i - 1][j - 1], min(dp[i - 1][j], dp[i][j - 1])) + 1;
}
}
printf("%d\n", dp[len1][len2]);
return 0;
}
|
一道递归题。
每次遇到左括号就开始递归,遇到右括号或者超出范围就停止。
部分数据存在括号不匹配的问题,我原代码会因为这个问题而超时两个点。
因为原代码有一部分是放在主函数里的,且这部分没有做超出范围的处理,会被括号不匹配卡掉。
后面把所有部分都塞到$DFS$函数里面就好了。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
|
#include <bits/stdc++.h>
#define maxn 100005
using namespace std;
int len, ans;
string str;
struct RE{
int pos;
int maxx;
};
RE dfs(int s){
int now = 0, maxx = 0, endpos = -1;
for(int i = s + 1; i <= len - 1; i++)
{
if(str[i] == '(')
{
RE tmp = dfs(i);
i = tmp.pos;
now += tmp.maxx;
}
else if(str[i] == '|')
{
maxx = max(maxx, now);
now = 0;
}
else if(str[i] == 'x')
{
now++;
}
else if(str[i] == ')')
{
maxx = max(maxx, now);
endpos = i;
break;
}
}
return (RE){endpos, max(maxx, now)};
}
int main(void)
{
cin >> str;
str = '(' + str + ')';
len = str.length();
cout << dfs(0).maxx << endl;
return 0;
}
|
一道数论题,[NOIP2017 小凯的疑惑]和[蓝桥杯2013省赛 买不到的数目]考察知识点相同。
由于遇到多次,所以利用$OneNote$顺便整理一份证明如下:

这个问题在国外好像又称为麦乐鸡问题。
在这道题里面数论的作用主要是用来证明这道题是否存在无限个包子数目不能凑出,剩下部分使用完全背包求解即可。
如果不会数论呢?
首次开这道题的时候我并没有想到怎么证明上界(早知道应该打表试试),于是使用了很暴力的方法:
只要上界足够大,那么若存在无限个凑不出的包子数目,则凑不出的包子数目也会很大。
由此,只要估计一个界。使得在足够大的上界下,不能凑出的包子数目大于这个界,就可以说明存在无限个凑不出的包子数目。
这并不是个完善的解,但能够有效得分。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
#include <bits/stdc++.h>
#define maxn 105
#define maxm 500005
using namespace std;
int n, a[maxn], dp[maxm];
int main(void)
{
scanf("%d", &n);
for(int i = 1; i <= n; i++)
scanf("%d", &a[i]);
dp[0] = 1;
for(int i = 1; i <= n; i++)
for(int j = a[i]; j <= maxm - 5; j++)
dp[j] |= dp[j - a[i]];
int cnt = 0;
for(int i = 1; i <= maxm - 5; i++)
if(!dp[i]) cnt++;
if(cnt > 5000)
printf("INF\n");
else
printf("%d\n", cnt);
return 0;
}
|
由相应数论知识,对于线性方程$a_1x_1+a_2x_2+a_3x_3+…+a_nx_n=c$,若存在整数解,则必须满足$gcd(a_1,a_2,a_3,…,a_n) \ | \ c$。由此,在读入完成后就能判断是否有无限个凑不出的数目。
然后,确定凑不出数目的最大值是多少。运用上面的数学证明,可以得到理论上界为99*100-99-100,在这里我们直接取到$10000$即可。
最后,使用完全背包,递推一遍,统计能够凑出来的数目(货物重量)即可。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| #include <bits/stdc++.h>
#define maxn 105
#define maxm 10005
using namespace std;
int n, g, a[maxn], dp[maxm];
int main(void)
{
scanf("%d", &n);
for(int i = 1; i <= n; i++)
scanf("%d", &a[i]);
g = a[1];
for(int i = 2; i <= n; i++)
g = __gcd(g, a[i]);
if(g != 1)
{
printf("INF\n");
return 0;
}
dp[0] = 1;
for(int i = 1; i <= n; i++)
for(int j = a[i]; j <= maxm - 5; j++)
dp[j] |= dp[j - a[i]];
int cnt = 0;
for(int i = 1; i <= maxm - 5; i++)
if(!dp[i]) cnt++;
printf("%d\n", cnt);
return 0;
}
|
二分答案入门板子题。
切割出来的巧克力是正方形的,因此直接二分边长,判断能有多少巧克力被切出即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| #include <bits/stdc++.h>
#define maxn 100005
using namespace std;
int n, k, h[maxn], w[maxn];
bool check(int now){
int cnt = 0;
for(int i = 1; i <= n; i++)
{
int maxx = max(h[i], w[i]);
int minn = min(h[i], w[i]);
if(maxx < now)
continue;
cnt += (maxx / now) * (minn / now);
}
return cnt >= k;
}
int main(void)
{
scanf("%d %d", &n, &k);
for(int i = 1; i <= n; i++)
scanf("%d %d", &h[i], &w[i]);
int lf = 1, rt = 100000, ans = -1;
while(lf <= rt)
{
int mid = (lf + rt) / 2;
check(mid) ? ans = mid, lf = mid + 1 : rt = mid - 1;
}
printf("%d\n", ans);
return 0;
}
|
说实话写完上一题板子一样的二分答案,再看到这一题…
不会真的考我线段树维护扫描线吧。
然后由于当时确实不会写,于是把数组开到$3000 * 3000$,使用模拟直接搞了一波。
提交后得$50pts$,遂观察别人的答案。
发现只要类型改为$bool$就可以开到$10000 * 10000$,学习了。
以前只大概记得$int$能开到$3000 3000$上下,再高就要炸了,$short$可以开到$5000 5000$,$bool$还真没怎么留意过。
实际我们可以计算一下,$\frac{10000 10000 1}{3000 3000 4} = 2.77…$,相差并不很大。
小技巧$get$。
于是我们就可以写出暴力程序了。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
#include <bits/stdc++.h>
#define maxn 10005
using namespace std;
int n, xi[maxn], yi[maxn];
bool board[maxn][maxn];
int main(void)
{
scanf("%d", &n);
for(int i = 1; i <= 2 * n; i++)
scanf("%d %d", &xi[i], &yi[i]), xi[i]++, yi[i]++;
for(int k = 1; k <= 2 * n; k += 2)
{
if(xi[k] > xi[k + 1]) swap(xi[k], xi[k + 1]);
if(yi[k] > yi[k + 1]) swap(yi[k], yi[k + 1]);
for(int i = xi[k]; i <= xi[k + 1] - 1; i++)
for(int j = yi[k]; j <= yi[k + 1] - 1; j++)
board[i][j] = true;
}
int cnt = 0;
for(int i = 1; i <= maxn - 5; i++)
for(int j = 1; j <= maxn - 5; j++)
if(board[i][j]) cnt++;
printf("%d\n", cnt);
return 0;
}
|
到这里就结束了吗?
当然不。
既然遇到了扫描线,那又怎么能轻易放过呢。
求矩阵面积并本来就是扫描线的经典应用,于是今天就顺便学习了一下,有一说一,比我之前想的要简单。
如果想通了其实还是很好写的。
扫描线的写法推荐$Luogu$模板题第一篇,写的很好,我就是从那里学习而来的U•ェ•*U。
求周长还暂时不会,下次遇到就学(咕咕咕)。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
|
#include <bits/stdc++.h>
#define maxn 3000005
#define int long long
#define lson(x) (x << 1)
#define rson(x) (x << 1) + 1
using namespace std;
int n, ans, tot, mp[maxn];
struct SegTree{
int lf, rt;
int sum, len;
} tree[maxn];
struct ScanLine{
int lf, rt, h;
int mark;
bool operator < (const ScanLine &A) const{
return h != A.h ? h < A.h : mark > A.mark;
}
} SL[maxn];
void pushup(int now){
if(tree[now].sum)
tree[now].len = mp[tree[now].rt + 1] - mp[tree[now].lf];
else
tree[now].len = tree[lson(now)].len + tree[rson(now)].len;
}
void EditSeg(int now, int lf, int rt, int k){
int nlf = mp[tree[now].lf], nrt = mp[tree[now].rt + 1];
if(nlf >= rt || nrt <= lf)
return;
if(nlf >= lf && nrt <= rt)
{
tree[now].sum += k;
pushup(now);
return;
}
EditSeg(lson(now), lf, rt, k);
EditSeg(rson(now), lf, rt, k);
pushup(now);
}
void Build(int now, int lf, int rt){
if(lf > rt) return;
tree[now].lf = lf;
tree[now].rt = rt;
tree[now].sum = 0;
tree[now].len = 0;
if(lf == rt) return;
int mid = (lf + rt) / 2;
Build(lson(now), lf, mid);
Build(rson(now), mid + 1, rt);
}
signed main(void)
{
scanf("%lld", &n);
for(int i = 1; i <= n; i++)
{
int xx1, xx2, yy1, yy2;
scanf("%lld %lld %lld %lld", &xx1, &yy1, &xx2, &yy2);
if(xx1 > xx2) swap(xx1, yy1);
if(yy1 > yy2) swap(yy1, yy2);
if(xx1 == xx2 || yy1 == yy2) continue;
mp[i] = xx1;
mp[i + n] = xx2;
SL[i] = (ScanLine){xx1, xx2, yy1, 1};
SL[i + n] = (ScanLine){xx1, xx2, yy2, -1};
}
n <<= 1;
sort(mp + 1, mp + n + 1);
sort(SL + 1, SL + n + 1);
tot = unique(mp + 1, mp + n + 1) - mp - 1;
Build(1, 1, tot - 1);
for(int i = 1; i <= n - 1; i++)
{
EditSeg(1, SL[i].lf, SL[i].rt, SL[i].mark);
ans += tree[1].len * (SL[i + 1].h - SL[i].h);
}
printf("%lld\n", ans);
return 0;
}
|
小结
第一轮的蓝桥刷下来了,说实话,比我想得要难不少。
为了省赛不白给,确实需要进一步的努力啊。
然后就是通过真题认识了一下,这玩意不是按难度排的…
第三题魔方贼难写,第九题二分有手就行…
下一把复盘在路上了,再接再厉U•ェ•*U


