背景

日常补之前比赛的题目，剩下三道，一个数论，一个数据结构，还剩下就是这一个。前面比赛都是补到八个可做题，这场好像还可以再写多点？看讲解看到是尺取接下来就想自己实现一下。

不过刚刚看了一下数据结构那题的讲解，是我菜了，没想到转化问题

题目

image-20210304202805591

写题思路

刚开始写的时候，觉得如果要得到等级$A$的不超过$k$个，则需要尽可能让他们得$B,C,D,E$，但是样例告诉我这样写并不能$AC$该题：

$INPUT$

1
2
3
4
3 1
100 100 100 100 100
1000 99 99 99 99 
101 1 1 1 1

$OUTPUT$

1
2

从样例我们知道，学生的$B$等级分数可能很高也可能很低。

也就是说，并不像平时我们的认知一样，得$A$的学生的分数一定比得$B$的学生分数要高，得$B$的学生分数可能也会很高。

此时，我想通过根据$B$成绩排序的思路就戛然而止了。

后面搞了几种奇怪的贪心方法，但是都很难过这样的样例。于是去瞄了讲解。

讲解讲到，维护分数最大值和最小值和使用尺取法时，退出，准备接着思路写一下。

要维护分数最大最小值，也就是要把每个人的五个分数都放入循环中。此时考虑设计需要维护的量，以及如何存放数据，草稿如下：

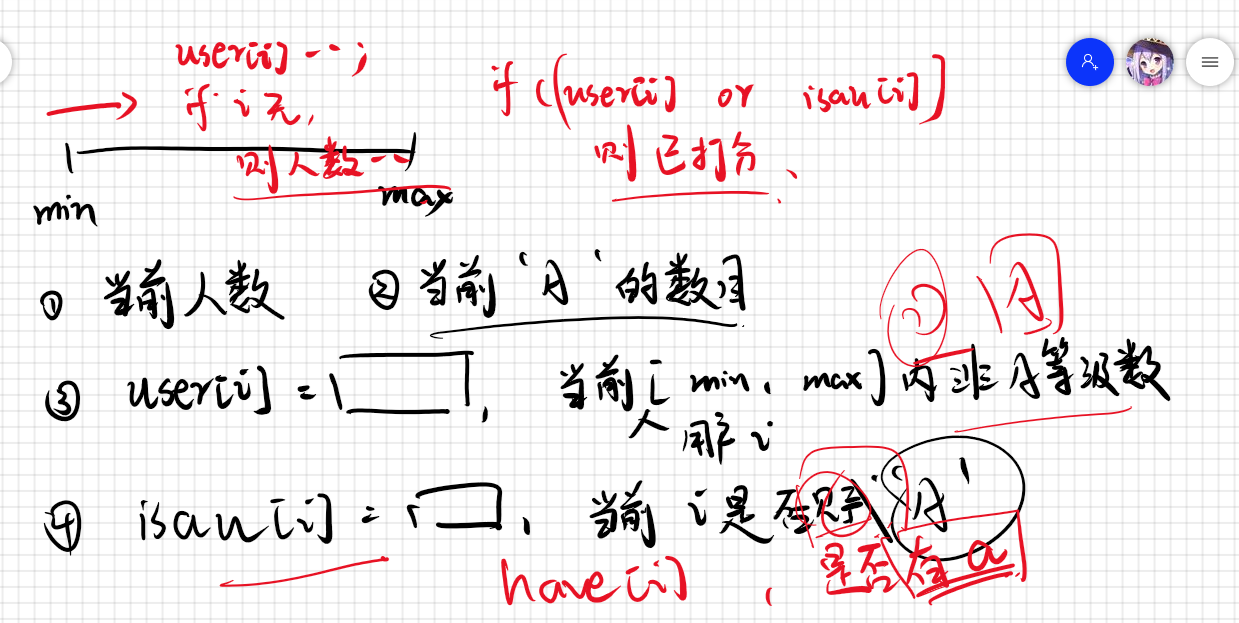
image-20210304203601485

简单概括该图内容如下：

  • 结构体存放每人分数，维护变量有是否为A等级，对应的学生编号，对应的预期成绩；
  • user[i]存放学生$i$，在当前区间$[minn,maxx]$中，有多少项非A的成绩；
  • isau[i]（后改名为hava[i]）存放区间内是否存在学生$i$的A项成绩；
  • 当前人数，后命名为num_p；当前$A$的数目，后命名为num_a。

通过维护这些量，我们可以得到：

  • 若区间$[minn,maxx]$内没有某个学生$i$的成绩，则hava[i] == 0 && user[i] == 0。
  • 若区间$[minn,maxx]$内总人数num_p等于$n$，则说明这个区间能够给每一学生都打分，更新答案
  • 若区间$[minn,maxx]$内$A$的数目超过$k$，则$break$，移动左区间端点

然后考虑，每次左区间端点移动需要删除什么量，右区间端点移动需要增加什么量：

分类讨论如下：

  • 左区间端点移动时，删除左区间端点对应的学生$i$的成绩$S$：

① 如果$S$是学生$i$的非$A$的成绩项，则令$user[i]$减去$1$，此时判断：

若user[i] == 0 && hava[i] == 0，则左移后区间内无学生$i$的成绩，当前人数$-1$

若user[i] == 0 && hava[i] == 1，则只剩下$A$等级成绩，当前$A$的数目$+1$

否则，不需要改变当前人数和当前$A$的数目，继续操作

② 如果$S$是学生$i$的$A$的成绩项，则令$hava[i]=0$，此时判断：

若 user[i] == 0 && hava[i] == 0 ，则左移后区间内无学生$i$的成绩，当前人数$-1$

否则，不需要改变当前人数和当前$A$的数目，继续操作

  • 右区间端点移动时，添加右区间端点对应的学生$i$的成绩$S$：

（在我的写法中，需要额外维护一个inq[i]，说明i是否已经被添加过）

① 如果$S$是学生$i$的非$A$的成绩项，令$user[i]$加一，此时判断：

若区间内hava[i] == 0 && user[i] == 0，则区间内无学生$i$的成绩，则人数加$1$。

② 如果$S$是学生$i$的$A$的成绩项，令$hava[i]=1$，此时判断：

若区间内hava[i] == 0 && user[i] == 0，则区间内无学生$i$的成绩，人数加$1$，且$A$的数目加一。

将分类讨论转化为代码，得到：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
#include <bits/stdc++.h>
const int maxn = 1e6 + 5;
using namespace std;
int n, k, ans = (1 << 30), ed[maxn];
int num_p, num_a, user[maxn], hava[maxn], inq[maxn];
struct val{
    int p;
    int sc;
    bool isa;
}v[maxn];
bool cmp(const val &A, const val &B){
    if(A.sc == B.sc)
        return A.p == B.p ? A.isa < B.isa : A.p < B.p; 
    return A.sc < B.sc;
}
int main(void)
{
    scanf("%d %d", &n, &k);
    for(int i = 1; i <= n; i++)
    {
        int a, b, c, d, e;
        scanf("%d %d %d %d %d", &a, &b, &c, &d, &e);
        v[i].p = i; v[i].sc = a; v[i].isa = true;
        v[i + n].p = i; v[i + n].sc = b; v[i + n].isa = false;
        v[i + 2 * n].p = i; v[i + 2 * n].sc = c; v[i + 2 * n].isa = false;
        v[i + 3 * n].p = i; v[i + 3 * n].sc = d; v[i + 3 * n].isa = false;
        v[i + 4 * n].p = i; v[i + 4 * n].sc = e; v[i + 4 * n].isa = false;
    }
    sort(v + 1, v + 5 * n + 1, cmp);
    ed[0] = 1;
    for(int i = 1; i <= 5 * n; i++)
    {
        if(ed[i - 1] == -1)    break;
        for(int j = ed[i - 1]; j <= 5 * n; j++)
        {
            if(!inq[j])
            {
                inq[j] = 1;
                if(user[v[j].p] == 0 && hava[v[j].p] == 0)
                {
                    num_p++;
                    if(v[j].isa)
                    {
                        hava[v[j].p] = 1;
                        num_a++;
                    }
                    else
                        user[v[j].p]++;
                }
                else
                {
                    if(v[j].isa)
                        hava[v[j].p] = 1;
                    else
                    {
                        //if(hava[v[j].p])    num_a--;
                        user[v[j].p]++;
                    }
                }
            }
            if(num_a > k)
            {
                ed[i] = j;
                break;
            }
            if(num_p == n)
            {
                ans = min(ans, v[j].sc - v[i].sc);
                //printf("%d %d %d\n", i, j, ans);
                ed[i] = j;
                break;
            }
            if(j == 5 * n)    ed[i] = -1;
        }
        if(v[i].isa)
        {
            hava[v[i].p] = 0;
            if(user[v[i].p] == 0)    num_p--;
        }
        else
        {
            user[v[i].p]--;
            if(hava[v[i].p] && user[v[i].p] == 0)    num_a++;
            else if(user[v[i].p] == 0 && hava[v[i].p] == 0)    num_p--;
        }
    }
    printf("%d\n", ans);
    return 0;
}

即可$AC$该题。

别的

这道题后面我去看了官方标程，实现的思路大体和我一样，不过要简洁一些。

讨论区还有用最小堆维护的贪心做法：

出自@神崎兰子

image-20210304220144165

不过这份题解的标黄部分没有怎么看懂，看了一下代码也好像没有这一块…其他倒是很清晰…

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include<bits/stdc++.h>
using namespace std;
struct node{
    int id,i,val;
    node(int id,int i,int val){this->id=id,this->i=i,this->val=val;}
    bool operator < (const node &b)const
    {
        return val>b.val;
    }
};
priority_queue<node>q;
int a[100010][5];
int main(){
    int n,k,i,j,cnt=0,ma=0;
    cin>>n>>k;
    for(i=0;i<n;i++){
        for(j=0;j<5;j++)scanf("%d",&a[i][j]);
        node temp(i,4,a[i][4]);
        q.push(temp);
        ma=max(ma,a[i][4]);
    }
    int res=ma-q.top().val;
    while(1){
        node temp=q.top();
       // cout<<temp.id<<" "<<temp.i<<" "<<temp.val<<endl;
        q.pop();
        if(temp.i==0)break;
        node ne(temp.id,temp.i-1,a[temp.id][temp.i-1]);
        q.push(ne);
        ma=max(ma,a[temp.id][temp.i-1]);
        if(temp.i==1)k--;
        if(k<0)break;
        res=min(res,ma-q.top().val);
    }
    cout<<res;
}

最后

感觉还是比较不错的，因为$inq$的问题调了好久，不过最后调出来一发就过了hhh…

希望能变得更强？U•ェ•*U