题意

给定一个有$n$个元素的集合$S$，求所有$S$的非空子集$B$中$max(B) * min(B)$的和。

$n \leq 2 * 10^5$。

$max(B)$指子集$B$中最大的元素。

思路

要计算两个值，优先考虑固定其中的一个，尝试计算另外一个。

假设固定了$max$，要求枚举所有的$min$，并计算除了必选的$max$和$min$外元素的子集数为多少。

如${2,3,4,5}$，当$max=5,min=2$时，中间有两个元素$3,4$可选，则子集数为$2^2$，总贡献为$5 2 2^2$。

时间复杂度为$O(n^2 logn)$，不能通过该题。

后面考虑优化，观察到某些元素的贡献似乎都与$2^n$有关，如当$max=5$时，贡献为：

现在要做的就是快速计算后半段$5 (4 2^0 + 3 2^1 + 2 2 ^2)$。

看到这条式子，有点想到字符串$hash$（事实上就是$hash$预处理的部分），但还没理清子集的选择部分。不过这时我的队友已经搞出来了，并归纳成了三步走。

初始，我们将$t,ans$置为$0$，排序后如下：

  1. $ans = ans + a[i] * a[i]$
  2. $ans = ans + t * a[i]$
  3. $t = 2 * t + a[i]$

或者更形象的，我们用图来表示：

$t$代表红色下划线表示的部分。

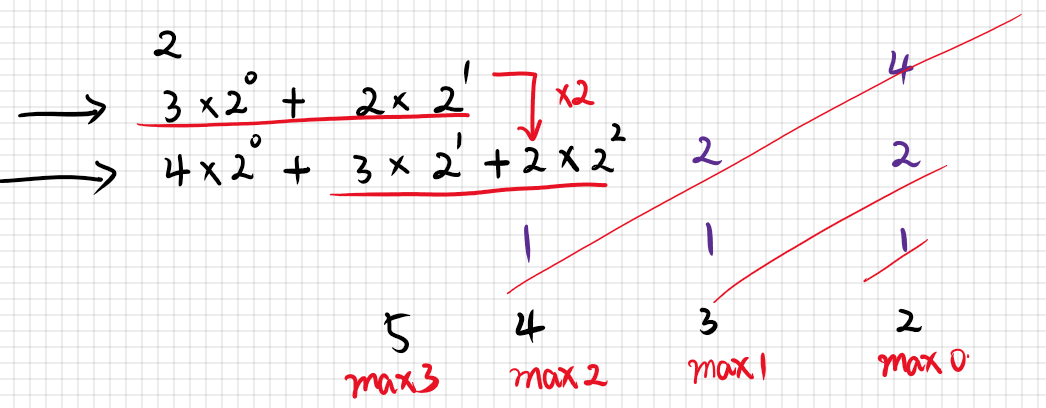
image-20210331132231508

由此，就可以用很短代码解决这个问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <bits/stdc++.h>
#define maxn 200005
#define mod 998244353
#define int long long
using namespace std;
int n, ans, a[maxn];
signed main(void)
{
    scanf("%lld", &n);
    for(int i = 1; i <= n; i++)    scanf("%lld", &a[i]);
    sort(a + 1, a + n + 1);
    int t = 0;
    for(int i = 1; i <= n; i++)
    {
        ans = (ans + a[i] * a[i]) % mod;
        ans = (ans + t * a[i]) % mod;
        t = (2 * t + a[i]) % mod;
    }
    printf("%lld\n", ans % mod);
    return 0;
}

别的

虽然有一说一我的某个队友常年摸鱼搞项目，但是他的思维确实是很有逻辑性的。每次我们在口胡的时候还得好好靠他才能推到正解…

嗯要天梯赛要蓝桥杯要$ICPC$了，有点麻…

现在还压了三道题没补，补完就去肝天梯了…