题意

现在有$N$个人，这$N$个人编号分别为$1-n$，每个人的重量为$a_i$。同时，每个人手上拿着编号为$p_i$的行李，${p_i}$为$n$的一个排列。同时，对于编号为$i$的行李，其重量为$b_i$。

现在需要你找到一个方案，对他们的行李两两交换，使得编号为$i$的人拿到编号为$i$的行李，且交换次数最少。而且，如果某个人拿到的行李重量大于自身重量$a_i$时，这个人将不能再参与到后面的交换中。

思路

开始的时候理解题意理解了很久。这种题属于变量比较多的题目，想起来比较麻烦。

后面感觉是一个图论题，应该是要寻找环，然后环内的元素可以完成两两交换。

但是没有理清$p_i$的关系，不知道怎么建图会比较好，也不清楚怎么构造两两交换，于是就结束了。

后学习题解，发现要慢慢拆分这个问题会比较好。

  • 首先，如果在最初状态，存在$b[p[i]] \geq a[i]$，且$p[i] \neq i$，则一定无解。如果不存在那样的情况，则一定存在一个解在满足最小交换次数的情况下使得$i=p[i]$，原因见下文。

  • 其次，由于要进行交换，考虑对于$(i, p[i])$进行连边，并以此类推。即$(i \rightarrow p[i] \rightarrow p[p[i]] \rightarrow \dots)$。

  • 然后，观察这样建成的图，发现由于${p_i}$是一个排列，因此这张图由多个互不相交的环组成（包括自环）。

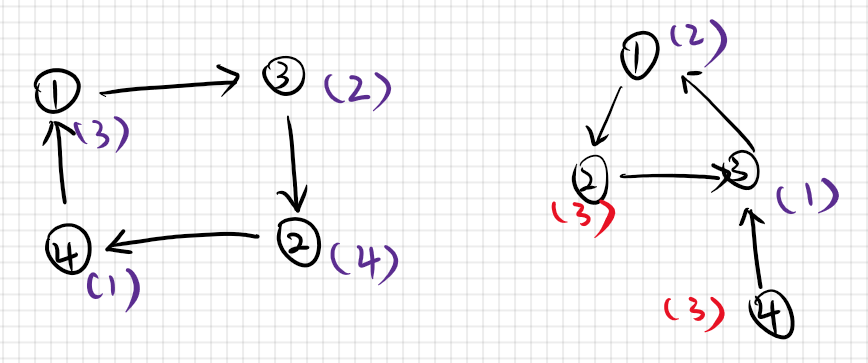
image-20210401125303036

  • 每一个环都是独立的，不会影响其他环的结果。同时，环内元素均可以通过两两交换达到$i=p[i]$，且存在一种方法在满足最小交换次数的情况下能够实现$i=p[i]$。原因见下文。

我们上面提到了一种构造方法，能够解决最小交换次数的问题，详细操作步骤如下：

  1. 对于环内的元素的$a[i]$进行排序，设$a[i]$最小的元素为$G$，优先满足$G$能够实现$i=p[i]$。
  2. 由前提条件，环内不存在满足$b[p[i]] \geq a[i]$的元素，也就是说，$G$一定能够进行一次交换。并且与$G$进行交换的元素$G’$也一定能够接着进行交换。（$G’.a[i] \geq G.a[i] > b[p[i]]$）
  3. 依照这样的步骤，每次都找最小的且未回到应到位置上的元素，就可以在$size-1$次操作下，把当前环内元素通过两两交换使其均满足题意。

对于某个单一的环，操作次数为$size-1$，而对于所有的环，有最终答案为$N-C$，其中$C$为环的个数。如此，问题转化为建图后图内有多少个环，只需要$dfs$一遍，并在寻找到环的时候使用我们上面构造的方案记录交换的每一步即可。

在寻找到环后，我们需要交换$a[i]$最小的元素$G$，以及满足$p[i]=G$的某个元素$G’$。因此，我们需要一个数组$nxt[i]$，意义为$nxt[p[i]]=G’$，即记录$p[i]$现在被哪个元素所持有。

于是，总结前文，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include <bits/stdc++.h>
#define maxn 400005
using namespace std;
int n, pcnt, acnt, a[maxn], b[maxn], p[maxn], nx[maxn], vis[maxn];
pair<int, int> ans[maxn];
struct pe{
    int pos;
    int wei;
}np[maxn];
bool cmp(const pe &A, const pe &B){
    return A.wei < B.wei;
}
void dfs(int x){
    if(vis[x])
    {
        sort(np + 1, np + pcnt + 1, cmp);
        for(int i = 1; i <= pcnt; i++)
        {
            int now = np[i].pos, nxt = nx[np[i].pos];
            if(now == nxt)    continue;
            swap(p[now], p[nxt]);
            nx[p[now]] = now;
            nx[p[nxt]] = nxt;
            ans[++acnt] = make_pair(now, nxt);
        }
    }
    else
    {
        vis[x] = 1;
        np[++pcnt] = (pe){x, a[x]};
        dfs(p[x]);
    }
}
int main(void)
{
    scanf("%d", &n);
    for(int i = 1; i <= n; i++)
        scanf("%d", &a[i]);
    for(int i = 1; i <= n; i++)
        scanf("%d", &b[i]);
    int flag = 0;
    for(int i = 1; i <= n; i++)
    {
        scanf("%d", &p[i]);
        nx[p[i]] = i;
        if(a[i] <= b[p[i]] && i != p[i])    flag = 1;
    }
    if(flag)    
    {
        printf("-1\n");
        return 0;
    }
    for(int i = 1; i <= n; i++)
    {
        pcnt = 0;
        if(!vis[i])    dfs(i);
    }
    printf("%d\n", acnt);
    for(int i = 1; i <= acnt; i++)
        printf("%d %d\n", ans[i].first, ans[i].second);
    return 0;
}

别的

好耶，暂时补完题了，要去肝天梯赛了U•ェ•*U