Codeforces 1498C - Planar Reflections

题意

对于$t$组询问，每组询问给出两个数$n,k$，代表挡板的个数$n$和粒子的能量$k$。

粒子在冲向一个挡板的时候，有两种可能：

1. 直接冲过挡板，能量不损失
2. 与挡板碰撞，能量$k$减少$1$，粒子的飞行变为反向（当$k=1$时，粒子不会发生碰撞）

问最后有多少种可能的粒子轨迹，答案对$1e9+7$取模。

为更清晰说明，附上图例一张，不同颜色代表不同的粒子轨迹。

---

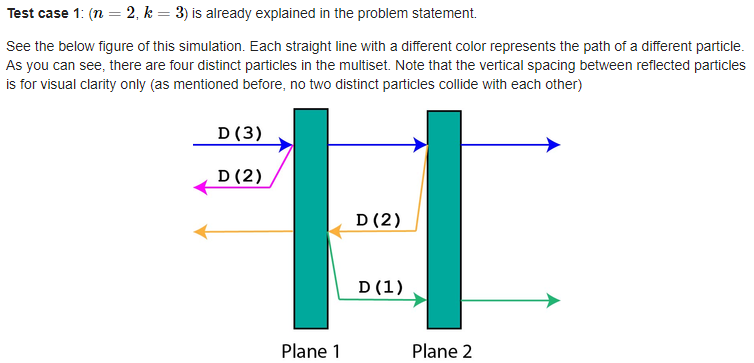
思路

这道题明显可以使用动态规划来解决，但是如何设计方程是个问题。

最开始的时候，我把粒子飞行方向也考虑了进去。

设计$dp[n][k][0/1/2/3]$，其中：

$0$代表前方有$n$个板，当前剩余$k$点能量，飞行方向为正向

$1$代表前方有$n$个板，当前剩余$k$点能量，飞行方向为反向

$2$代表在前方有$n$个板时发生碰撞，碰撞前剩余$k$点飞行能量，碰撞前飞行方向为正向

$3$代表在前方有$n$个板时发生碰撞，碰撞前剩余$k$点飞行能量，碰撞前飞行方向为反向

理论上，这个$dp$应该是能够转移好的，最终答案为$dp[n][k][0]$，但是这样的转移方式过于复杂，我们似乎并不需要维护一个方向。

后面设计，$dp[n][k]$，$n$为当前方向还剩余多少板子，$k$为当前粒子的能量，有：

$$dp[n][k]=dp[G-n][k - 1] + dp[n - 1][k]$$

由此，设计记忆化搜索，即可$AC$。

需要特别注意的是，在不同的询问中，$dp[n][k]$的结果不一定是一样的，因此需要每组询问前清空一下$dp$数组。

代码

#include <bits/stdc++.h>
#define maxn 1005
#define int long long
using namespace std;
int dp[maxn][maxn];
int t, n, k;
const int mod = 1e9 + 7;
int dfs(int now, int can){
    if(~dp[now][can])    
        return dp[now][can];
    if(now == 0)
        return dp[now][can] = 1;
    if(can == 1)
        return dp[now][can] = 1;
    int val = 0;
    val = (val + dfs(n - now, can - 1)) % mod;
    val = (val + dfs(now - 1, can)) % mod;
    return dp[now][can] = val;
}
signed main(void)
{
    scanf("%lld", &t);
    while(t--)
    {
        memset(dp, -1, sizeof(dp));
        scanf("%lld %lld", &n, &k);
        printf("%lld\n", dfs(n, k));
    }
    return 0;
}

---

别的

昨日微风正好，阳光温和。这么好的日子，却有憨批握不住手机，滑落地上，哐当一声，黑屏关机。

无法，京东自营，价格排序，迅速下单平价机救火。

非常巧合，教练群竟也有人发表一篇，今日没有手机的感想。

下单机器事小，重新配置机上的软件事大。

登录账号配置邮箱，安装各种$app$，人快麻了。

还有日常微信好友验证，天！

搞完已凌晨一点，睡下，才发现一天都在忙活这个，一题没过，真是羞愧难当…

UPDATE 2021.05.10

搜其他题题解时，发现该题有很多种$dp$方法，这里也记录一下，比如：

来源：@xloypaypa

End