前言

被各路神仙暴打。

有一说一，周五周日牛客多校，周二周四杭电多校，确实很让人吃紧（

看群友们好像两边都坚持打，而且补题也补得很快（

目前还没复盘杭电多校…或许以后会去。

复盘

C - Draw Grids

签到题。读完题就可以写了，大概就是模拟一下生成树。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/* vegetable1024 | oi-liu.com | Maybe Lovely? */

#include <bits/stdc++.h>
#define maxn 800005
#define int long long
using namespace std;
int n, m;
int read(){
    int x = 0; char ch = getchar();
    while(ch < '0' || ch > '9')    ch = getchar();
    while(ch >= '0' && ch <= '9')  x = x * 10 + ch - '0', ch = getchar();
    return x;
}

signed main(void)
{
    n = read(); m = read();
    int lk = (n - 1) * m + (m - 1);
    printf(lk & 1 ? "YES\n" : "NO\n");
    return 0;
}

D - Er Ba Game

同样是签到题，模拟题意就可以了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
/* vegetable1024 | oi-liu.com | Maybe Lovely? */

#include <bits/stdc++.h>
#define maxn 800005
#define int long long
using namespace std;
int t, a1, b1, a2, b2;
int read(){
    int x = 0; char ch = getchar();
    while(ch < '0' || ch > '9')    ch = getchar();
    while(ch >= '0' && ch <= '9')  x = x * 10 + ch - '0', ch = getchar();
    return x;
}
int calc(int a, int b){
    if(a == 2 && b == 8)
        return 99999;
    if(a == b)
        return a * 1000;
    return 0;
}
signed main(void)
{
    t = read();
    while(t--)
    {
        a1 = read(); b1 = read();
        a2 = read(); b2 = read();

        if(a1 > b1)    swap(a1, b1);
        if(a2 > b2)    swap(a2, b2);

        int pr1 = calc(a1, b1), pr2 = calc(a2, b2);
        if(pr1 != pr2)
            printf(pr1 > pr2 ? "first\n" : "second\n");
        else if(pr1 == pr2 && pr1)
            printf("tie\n");
        else
        {
            int v1 = (a1 + b1) % 10, v2 = (a2 + b2) % 10;
            if(v1 != v2)
                printf(v1 > v2 ? "first\n" : "second\n");
            else if(v1 == v2 && b1 != b2)
                printf(b1 > b2 ? "first\n" : "second\n");
            else
                printf("tie\n");
        }
    }
    return 0;
}

F - Girlfriend

计算几何，本质上是计算球缺的体积。

或许可以用积分推公式…不过用网上的球缺体积板子过掉了…

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
/* vegetable1024 | oi-liu.com | Maybe Lovely? */

#include <bits/stdc++.h>
#define maxn 800005
#define int long long
#define eps 1e-8
#define PI acos(-1.0)
using namespace std;
int t, k1, k2;
struct Point{
    double x, y, z;
}P[maxn];
double dis(Point a, Point b){
    return sqrt((a.x - b.x) * (a.x - b.x) + 
                (a.y - b.y) * (a.y - b.y) +
                (a.z - b.z) * (a.z - b.z));
}
int read(){
    int x = 0; char ch = getchar();
    while(ch < '0' || ch > '9')    ch = getchar();
    while(ch >= '0' && ch <= '9')  x = x * 10 + ch - '0', ch = getchar();
    return x;
}
void solve(double &rx, double &ry, double &rz, double &r, double a, double b, double c, double d, double e, double f, double k){
    rx = (k * k * d - a) / (k * k - 1);
    ry = (k * k * e - b) / (k * k - 1);
    rz = (k * k * f - c) / (k * k - 1);

    r = (k * k * (d * d + e * e + f * f) - (a * a + b * b + c * c)) / (k * k - 1);
    r = sqrt(rx * rx + ry * ry + rz *rz - r);
}
signed main(void)
{
    t = read();
    while(t--)
    {
        for(int i = 1; i <= 4; i++)
            scanf("%lf %lf %lf", &P[i].x, &P[i].y, &P[i].z);
        
        k1 = read(); k2 = read();

        double r1x, r1y, r1z, r1r, r2x, r2y, r2z, r2r;
        solve(r1x, r1y, r1z, r1r, P[1].x, P[1].y, P[1].z, P[2].x, P[2].y, P[2].z, k1);
        solve(r2x, r2y, r2z, r2r, P[3].x, P[3].y, P[3].z, P[4].x, P[4].y, P[4].z, k2);

        double disrr = dis((Point){r1x, r1y, r1z}, (Point){r2x, r2y, r2z});

        //printf("debug: %lf %lf %lf %lf %lf %lf %lf %lf\n", r1x, r1y, r1z, r2x, r2y, r2z, r1r, r2r);

        if(fabs(disrr - r1r - r2r) <= eps || disrr > r1r + r2r)
            printf("0.000\n");
        else if(disrr + r1r <= r2r)
            printf("%.3lf\n", 4.0 / 3.0 * PI * r1r * r1r * r1r);
        else if(disrr + r2r <= r1r)
            printf("%.3lf\n", 4.0 / 3.0 * PI * r2r * r2r * r2r);
        else
        {
            double cosa = (r1r * r1r + disrr * disrr - r2r * r2r) / (2 * r1r * disrr);
            double h1 = r1r * (1 - cosa);
            double cosb = (r2r * r2r + disrr * disrr - r1r * r1r) / (2 * r2r * disrr);
            double h2 = r2r * (1 - cosb);
            double V = PI / 3 * (3 * r1r - h1) * h1 * h1 +
                       PI / 3 * (3 * r2r - h2) * h2 * h2;
            printf("%.3lf\n", V);
        }

    }
    return 0;
}

I - Penguins

大模拟，其实还是蛮好写的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
/* vegetable1024 | oi-liu.com | Maybe Lovely? */

#include <bits/stdc++.h>
#define maxn 25
#define int long long
using namespace std;
string ans;
char board[5][maxn][maxn], fans[5][maxn][maxn], vis[maxn][maxn][maxn][maxn];
int d1y[] = {0, -1, 1, 0};
int d2y[] = {0, 1, -1, 0};
int dx[] = {1, 0, 0, -1};
struct Node{
    string st;
    int nst;
    int xx1, yy1;
    int xx2, yy2;
};
char read(){
    char ch = getchar();
    while(ch != '.' && ch != '#')   ch = getchar();
    return ch;
}
bool check(int xx, int yy, int k){
    return xx >= 1 && xx <= 20 && yy >= 1 && yy <= 20 && board[k][xx][yy] == '.';
}
void calc(Node now, int &xx1, int &yy1, int &xx2, int &yy2, int d){
    xx1 = now.xx1; yy1 = now.yy1; 
    xx2 = now.xx2; yy2 = now.yy2;
    
    if(check(xx1 + dx[d], yy1 + d1y[d], 1))
        xx1 = xx1 + dx[d], yy1 = yy1 + d1y[d];
    
    if(check(xx2 + dx[d], yy2 + d2y[d], 2))
        xx2 = xx2 + dx[d], yy2 = yy2 + d2y[d];
}
void tra(string res){
    int len = res.length();
    for(int i = 0; i < len; i++)
    {
        if(res[i] == '0')    putchar('D');
        if(res[i] == '1')    putchar('L');
        if(res[i] == '2')    putchar('R');
        if(res[i] == '3')    putchar('U');
    }
    putchar('\n');
}
void bfs(){
    queue<Node> q1;
    q1.push((Node){"", 0, 20, 20, 20, 1});
    while(!q1.empty())
    {
        Node now = q1.front(); q1.pop();
        //cout << "debug: " << now.nst << endl;
        //cout << "debug: " << " " << now.nst << " " << now.xx1 << " " << now.yy1 << " " << now.xx2 << " " << now.yy2 << '\n';
        //tra(now.st);
        //system("pause");
        if(now.xx1 == 1 && now.yy1 == 20 && now.xx2 == 1 && now.yy2 == 1)
        {
            ans = now.st;
            //tra(now.st);
            break;
        }
        for(int i = 0; i < 4; i++)
        {
            int nx1, ny1, nx2, ny2;
            calc(now, nx1, ny1, nx2, ny2, i);
            if(!vis[nx1][ny1][nx2][ny2])
            {
                vis[nx1][ny1][nx2][ny2] = 1;
                q1.push((Node){now.st + to_string(i), now.nst + 1, nx1, ny1, nx2, ny2});
            }
        }
    }
    //cout << ans << '\n';
}
void mk(){
    int len = ans.length();
    int px1 = 20, py1 = 20, px2 = 20, py2 = 1;
    for(int i = 0; i < len; i++)
    {
        //printf("debug: %d %d %d %d\n", px1, py1, px2, py2);
        fans[1][px1][py1] = 'A';
        fans[2][px2][py2] = 'A';
        calc((Node){"", 0, px1, py1, px2, py2}, px1, py1, px2, py2, ans[i] - '0');
    }
    fans[1][px1][py1] = 'A';
    fans[2][px2][py2] = 'A';   
}
signed main(void)
{
    for(int i = 1; i <= 20; i++)
    {
        for(int j = 1; j <= 20; j++)
            fans[1][i][j] = board[1][i][j] = read();
        for(int j = 1; j <= 20; j++)
            fans[2][i][j] = board[2][i][j] = read();
    }
    bfs();
    mk();
    cout << ans.length() << '\n';
    tra(ans);
    for(int i = 1; i <= 20; i++)
    {
        for(int j = 1; j <= 20; j++)
            printf(j == 20 ? "%c "  : "%c", fans[1][i][j]);
        for(int j = 1; j <= 20; j++)
            printf(j == 20 ? "%c\n" : "%c", fans[2][i][j]);
    }
    return 0;
}

J - Product of GCDs

欧拉降幂$Get$​

这道题难点应该主要在于如果推断一个数在$Gcd$​中的贡献，官方题解使用了一个很巧妙的办法：

考虑统计每个素因子的贡献。

首先欧拉筛求出范围内的素数，然后枚举素数以及素数次幂的倍数

​

在原序列中的出现次数。

更具体的对每一个$p^k$​的倍数，若其出现在序列中，则计数器$c=c+1$，枚举完$p^k$的每一倍数后，若$c \geq k$，则说明可以选择$(_k^c)$个集合，能够贡献的$gcd$为$p^k$。

但是，在$k$较小时，$p^k$的倍数可能与较大的$p^k$相重复。

不过，我们把目标放在求$p^1$的贡献，就不用在乎重复的问题了。此时只需要将所有不同的$k$的$p^k$的结果加起来得到$res$，再计算$p^{res}$​​​​​。

即：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
for(int i = 1; i <= s; i++)    
{
    xi[i] = read();
    cnt[xi[i]]++;
}
/* ... */
for(int i = 1; i <= PrimeSize; i++)
{
    int res = 0; //Pri[i]这个素因子总的贡献
    for(int j = pri[i]; j < maxn; j *= pri[i]) //枚举p^k
    {
        int c = 0;
        for(int l = j; l < maxn; l += j)    c += cnt[l]; //枚举c * p^k的出现次数
        if(c < k)     continue;
        res += C[c][k];    //选择GCD不小于p^k的方案数
        while(res >= phi + phi)    res -= phi;
    }
    if(res)
        ans = MUL(ans, qpow(pri[i], res, p), p);
}

由于$sum$可能很大，我们使用欧拉降幂即可。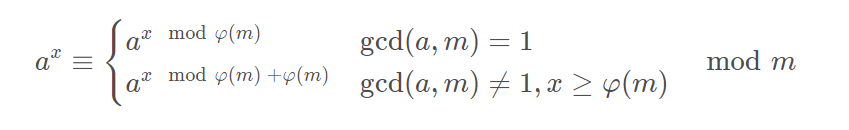image-20210827213923430

完整代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
/* vegetable1024 | oi-liu.com | Maybe Lovely? */

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int maxn = 8e4 + 5;
const int maxx = 1e7 + 5;

int t, p, s, k, phi, xi[maxn], cnt[maxn];
int cp, pri[maxx], C[maxn][35];
bool isp[maxx];

int read(){
    int x = 0; char ch = getchar();
    while(ch < '0' || ch > '9')    ch = getchar();
    while(ch >= '0' && ch <= '9')  x = x * 10 + ch - '0', ch = getchar();
    return x;
}
int eular(int val){
    int ans = val;
    for(int i = 1; i <= cp; i++)
        if(val % pri[i] == 0)
        {
            ans -= ans / pri[i];
            while(val % pri[i] == 0)    val /= pri[i];
        }
        if(val > 1)    ans -= ans / val;
    return ans;
}
void euler(int lim){
    memset(isp, true, sizeof(isp));
    for(int i = 2; i <= lim; i++)
    {
        if(isp[i])    pri[++cp] = i;
        for(int j = 1; j <= cp && i * pri[j] <= lim; j++)
        {
            isp[i * pri[j]] = false;
            if(i % pri[j] == 0)    break;
        }
    }
}
void inits(int lim){
    phi = eular(p);
    C[0][0] = 1;
    for(int i = 1; i <= lim; i++)   
    {
        C[i][0] = 1;
        for(int j = 1; j <= min(k, i); j++)
        {
            C[i][j] = C[i - 1][j] + C[i - 1][j - 1];
            while(C[i][j] >= phi + phi)
                C[i][j] -= phi;
        }
    }
}
int MUL(int x, int y, int p){
    return (__int128)x * y % p;
}
int qpow(int a, int b, int p){
    if(b == 0)
        return 1;
    int tmp = qpow(a, b / 2, p);
    tmp = MUL(tmp, tmp, p);
    if(b & 1)    tmp = MUL(tmp, a, p);
    return tmp;
}
signed main(void)
{
    euler(maxx);

    t = read();
    while(t--)
    {
        memset(cnt, 0, sizeof(cnt));

        s = read(); k = read(); p = read();
        for(int i = 1; i <= s; i++)    
        {
            xi[i] = read();
            cnt[xi[i]]++;
        }

        inits(s);

        int ans = 1;
        for(int i = 1; i <= cp; i++)
        {
            int res = 0;
            for(int j = pri[i]; j < maxn; j *= pri[i])
            {
                int c = 0;
                for(int l = j; l < maxn; l += j)    c += cnt[l];
                if(c < k)     continue;
                res += C[c][k];
                while(res >= phi + phi)    res -= phi;
            }
            if(res)
                ans = MUL(ans, qpow(pri[i], res, p), p);
        }
        printf("%lld\n", ans);
    } 
    return 0;
}

K - Stack

题意大概是给出一个单调栈，和$k$个时刻的单调栈的$size=b_{p_i}x_i$。问能不能构造一个入栈序列${a_i}$（同时也是一个排列）满足题目所给的条件。

学习了一种很妙的构造方法。

每次我们贪心的构造尽可能长的单调序列，这样才能更容易满足$len \geq size$的条件（弹出到$len=size$为止），同时对未给定的$b[i]$​进行填充（当前的序列长度）。

而后，我们用一个$cnt$​数组，统计每个长度出现了多少次，用于构造答案。

最后对$cnt$数组做一个前缀和，保证每个单调序列不会冲突。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
/* vegetable1024 | oi-liu.com | Maybe Lovely? */

#include <bits/stdc++.h>
#define maxn 1000005
#define int long long
using namespace std;
int n, k, b[maxn], cnt[maxn];
int read(){
    int x = 0; char ch = getchar();
    while(ch < '0' || ch > '9')    ch = getchar();
    while(ch >= '0' && ch <= '9')  x = x * 10 + ch - '0', ch = getchar();
    return x;
}

signed main(void)
{
    n = read(); k = read();
    for(int i = 1; i <= k; i++)
    {
        int pi = read(), xi = read();
        b[pi] = xi;
    }
    int now = 0;
    for(int i = 1; i <= n; i++)
    {
        now++;
        if(b[i] > 0)
        {
            if(now < b[i])
            {
                printf("-1\n");
                return 0;
            }
            now = b[i];
        }
        else    b[i] = now;
    }
    for(int i = 1; i <= n; i++)    cnt[b[i]]++;
    for(int i = 1; i <= n; i++)
        cnt[i] = cnt[i - 1] + cnt[i];
    for(int i = 1; i <= n; i++)
        printf(i == n ? "%d\n" : "%d ", cnt[b[i]]--);
    return 0;
}