题意

给定一个长度为$n$的序列$\lbrace a_n \rbrace$，问是否存在长度为$n$的序列$\lbrace b_n\rbrace $，使得序列${a_n}$中的每一个数$a_i$，都存在一组$(j, k)$（$j,k$可以相等），$b_j-b_k=a_i$，若有则输出$YES$，否则输出$NO$。

思路

本题很妙，题解是将序列转化到图的问题去理解。

我们将$a_i=b_j-b_k$​，看作从$b_j$​连一条有向边到$b_k$​​。

我们暂时忽略边的方向性，可以发现，当某个连边方式合法时，相当于存在一张$n$​​个点$n$​​条边的连通图，且其中一定有至少一个环。

我们可以设这个环中有$m$​​个顶点，顶点标号依次为$v_1,v_2,\dots,v_m$​​​​。

由于首尾相接，环的顶点应该满足这个条件：

​

如果考虑方向性：

  • $b_i - b_j = a_i, \text{an edge from (i) to (j)}$

  • $b_i - b_j = -a_i, \text{an edge from (j) to (i)}$​

由上，我们通过给$a_i$​​​分配正负值（等效于在$b$​​中对$b_j,b_k$​​​连边）或分配$0$​​​（环内不包括这个点），来实现连边和判断是否存在一个环，如下所示：

​

到这里，一个直接的办法是，由于$n$​​非常小，我们可以利用$3$​​进制对环的状态进行压缩。

首先，假设存在一个环，且大小为$m$。

然后，对于环内的点，我们可以设为$1,2,3,\dots,m$​，如下构造：

  • $b_1 = 0$
  • $b_2 = b_1 - s_1 * a_1$​
  • $b_3 = b_2 - s_2 * a_2$
  • $…$
  • $b_m = b_{m - 1} - s_{m - 1} * a_{m-1}$​

其中，$s_i \in \lbrace -1, 1\rbrace$​​​​​​，代表边的方向性。

对于$a_i = \lbrace 1,2,3,6\rbrace $的情况，$s_i = \lbrace 1,1,1,-1\rbrace $是其中一个方案：

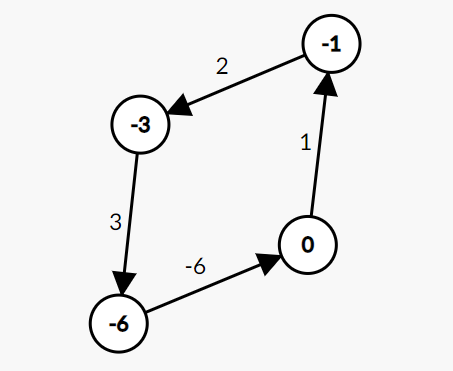
image-20210914165537239

由此，枚举每一种可能的情况，判断是否有环存在即可，时间复杂度$O(n3^n)$​。

本题也可使用背包实现。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
/* vegetable1024 | liushan.site | Maybe Lovely? */

#include <bits/stdc++.h>
#define maxn 800005
//#define int long long
using namespace std;

clock_t START_TIME, END_TIME;

//DEBUG TEMPLATE
template<typename T>
void Print(T value){
    std::cout << value << '\n';
}
template<typename Head, typename... Rail>
void Print(Head head, Rail... rail){
    std::cout << head << ", ";
    Print(rail...);
}

int read(){
    int x = 0; char ch = getchar();
    while(ch < '0' || ch > '9')    ch = getchar();
    while(ch >= '0' && ch <= '9')  x = x * 10 + ch - '0', ch = getchar();
    return x;
}

int t, n, a[maxn];
signed main(void)
{
    t = read();
    //START_TIME = clock();
    while(t--)
    {
        n = read();
        for(int i = 1; i <= n; i++)    a[i] = read();
        int mask = 1, gs = -1;
        for(int i = 1; i <= n; i++)    mask *= 3;
        for(int i = 1; i < mask; i++)
        {
            int ms = i, sum = 0;
            for(int k = 1; k <= n; k++)
            {
                int flag = ms % 3; ms /= 3;
                if(flag == 1)    sum += a[k] * 1;
                if(flag == 2)    sum += a[k] * (-1);
            }
            if(sum == 0){
                gs = 1;
                printf("YES\n");
                break;
            }
        }   
        if(gs == -1)    printf("NO\n");
    }
    //END_TIME = clock();
    //printf("%.5lf ms\n", (double)(END_TIME - START_TIME) / CLOCKS_PER_SEC * 1000);
    return 0;
}