线段树

线段树主要用于维护区间问题，常见应用如区间加，区间乘，区间最值等，还有一些其他应用，如区间开平方，求解最大子段和，最大连续子段长度等等。

虽然写起来没有树状数组轻便，但是实现起来很多时候思维难度要小于树状数组，也能完成某些树状数组完成不了的工作。

一般的线段树都是$O(nlogn)$的，但是某些经过特殊处理的线段树能够在某个方面（询问，或者区间赋值等）达到更优秀的复杂度，如珂朵莉树和猫树。

一些题目

🆗HDU1394

题意

给出一个长度为$n$的初始数列，你可以循环该数列，找到所有数列中逆序对最小的一个，并输出这个数列逆序对的个数。

循环该数列时，下标变化形如如：$[1,2,\dots,n] \rightarrow [2,3,\dots,n,1] \rightarrow \dots$

考察

单点修改+区间询问，逆序对

分析

首先求出初始数列的逆序对个数。维护一颗权值线段树，一边读入一边插入元素，插入完成后询问比该元素大的元素有多少个（Update(1, a[i], a[i], 1, tree); Query(1, a[i] + 1, n, tree)）。统计Query的和就为初始数列的逆序对个数。

然后，分析每次循环数列的贡献。

每次循环数列后，上一个数列最开始的元素会被转移到数列的末端。

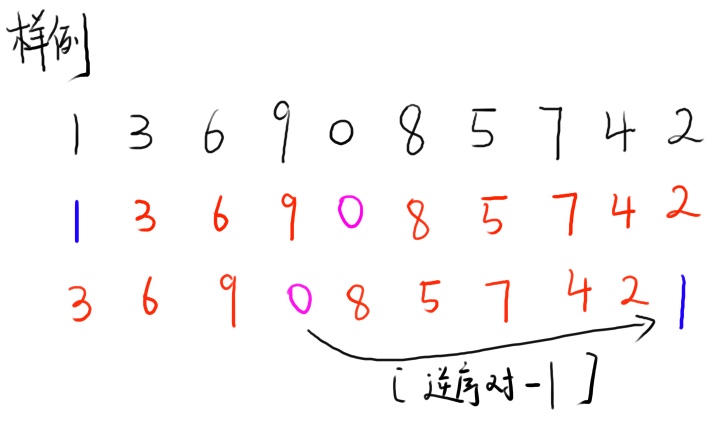
也就是说，逆序对个数会减少【比被转移元素小的元素个数】，增加【比被转移元素大的元素个数】。

原因如图所示（红色数字个数为增加的逆序对个数，粉色为减少的逆序对个数）：

image-20201212164630225

代码没有需要特别注意的地方，就是基础的线段树板子。

Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#include <bits/stdc++.h>
#define lson(x) (x << 1)
#define rson(x) (x << 1) + 1
#define maxn 100005
using namespace std;
int n, ans, a[maxn], cnt[maxn];
struct SegTree{
    int lf;
    int rt;
    int val;
} tree[maxn];
void Build(int now, int lf, int rt, SegTree t[])
{
    t[now].lf = lf;
    t[now].rt = rt;
    if (t[now].lf == t[now].rt)
    {
        t[now].val = 0;
        return;
    }
    int mid = (lf + rt) / 2;
    Build(lson(now), lf, mid, t);
    Build(rson(now), mid + 1, rt, t);
}
int Query(int now, int lf, int rt, SegTree t[]){
    if(lf <= t[now].lf && rt >= t[now].rt)
        return t[now].val;
    if(lf > t[now].rt || rt < t[now].lf)
        return 0;
    return Query(lson(now), lf, rt, t) + Query(rson(now), lf, rt, t);
}
void Update(int now, int lf, int rt, int k, SegTree t[]){
    if(lf >= t[now].lf && rt <= t[now].rt)
        t[now].val += k;
    if(lf > t[now].rt || rt < t[now].lf)
        return;
    Update(lson(now), lf, rt, k, t);
    Update(rson(now), lf, rt, k, t);
}
int main(void)
{
    while(~scanf("%d", &n))
    {
        ans = 0;
        memset(tree, 0, sizeof(tree));
        Build(1, 1, n, tree);
        for(int i = 1; i <= n; i++)
        {
            scanf("%d", &a[i]); a[i]++;
            Update(1, a[i], a[i], 1, tree);
            ans += Query(1, a[i] + 1, n, tree);
        }
        int minn = ans;
        for(int i = 1; i <= n; i++)
        {
            //printf("%d\n", ans);
            //printf("%d %d %d\n", i, Query(1, 1, a[i] - 1, tree), Query(1, a[i] + 1, n, tree));
            ans = ans - Query(1, 1, a[i] - 1, tree) + Query(1, a[i] + 1, n, tree);
            minn = min(minn, ans);
        }
        printf("%d\n", minn);
    }
    return 0;
}

🆗HDU1698

题意

有一初始值均为$1$的数列，现在每次指定区间$[a, b]$，将区间内的值替换为$1 \ or \ 2 \ or \ 3$，求最后该数列的和。

考察

区间赋值+区间询问

分析

只需要把线段树区间求和的模板，+=的部分改为=，就可以$AC$。

Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include <bits/stdc++.h>
#define maxn 4000005
#define lson(x) (x << 1)
#define rson(x) (x << 1) + 1
using namespace std;
int t, n, q, cases;
struct SegTree{
    int lf;
    int rt;
    int val;
    int lazy;
} tree[maxn];
void Build(int now, int lf, int rt){
    tree[now].lf = lf;
    tree[now].rt = rt;
    tree[now].lazy = 0;
    if (tree[now].lf == tree[now].rt)
    {
        tree[now].val = 1;
        return;
    }
    int mid = (lf + rt) / 2;
    Build(lson(now), lf, mid);
    Build(rson(now), mid + 1, rt);
    tree[now].val = tree[lson(now)].val + tree[rson(now)].val;
}
void Pushdown(int now){
    int mid = (tree[now].lf + tree[now].rt) / 2;
    tree[lson(now)].val = (mid - tree[now].lf + 1) * tree[now].lazy;
    tree[rson(now)].val = (tree[now].rt - mid) * tree[now].lazy;
    tree[lson(now)].lazy = tree[now].lazy;
    tree[rson(now)].lazy = tree[now].lazy;
    tree[now].lazy = 0;
}
void Add(int now, int lf, int rt, int k){
    if(lf <= tree[now].lf && rt >= tree[now].rt)
    {
        tree[now].val = (tree[now].rt - tree[now].lf + 1) * k;
        tree[now].lazy = k;
        return;
    }
    if(lf > tree[now].rt || rt < tree[now].lf)
        return;
    if(tree[now].lazy)    Pushdown(now);
    Add(lson(now), lf, rt, k);
    Add(rson(now), lf, rt, k);
    tree[now].val = tree[lson(now)].val + tree[rson(now)].val;
}
int Query(int now, int lf, int rt){
    if(lf <= tree[now].lf && rt >= tree[now].rt)
        return tree[now].val;
    if(lf > tree[now].rt || rt < tree[now].lf)
        return 0;
    if(tree[now].lazy)    Pushdown(now);
    return Query(lson(now), lf, rt) + Query(rson(now), lf, rt);
}
int main(void)
{
    scanf("%d", &t);
    while(t--)
    {
        scanf("%d", &n);  Build(1, 1, n);
        scanf("%d", &q);
        for(int i = 1; i <= q; i++)
        {
            int x, y, z;
            scanf("%d %d %d", &x, &y, &z);
            Add(1, x, y, z);
        }
        printf("Case %d: The total value of the hook is %d.\n", ++cases, Query(1, 1, n));
    }
    return 0;
}

🆗LG4513

题意

给出一个数列，有两种操作：

①选择其中一个项修改为任意值；

②求区间$[a,b]$中最大的子段和。

考察

单点修改+最大子段和

分析

最大子段和可以归为三种情况：

  • 该子段存在于目前线段树节点的左区间
  • 该子段存在于目前线段树节点的右区间
  • 该子段横跨了目前线段树节点的左右区间

要求最大子段和，可以考虑维护

  • 从区间左端点能够选出的最大子段和（一定包含左端点）（简称为$lmax$）
  • 从区间右端点能够选出的最大子段和（一定包含右端点）（简称为$rmax$）
  • 该区间内的最大子段和（无限制）（简称为$mx$）
  • 该区间内的元素和（简称为$sum$，若有左右儿子则分别为$lsum,rsum$）

其中：

先考虑边界情况：

在递归到目前节点只有一个元素时，有

$lmax=rmax=mx=sum当前元素$

然后考虑其他情况：

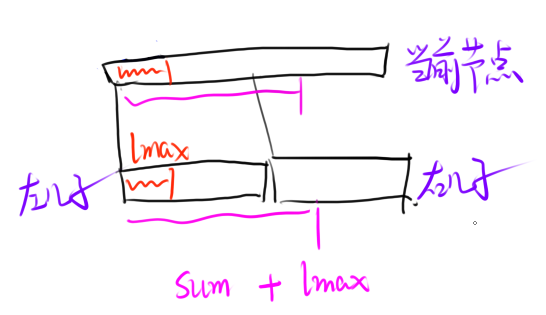
由于$lmax$一定要取到区间左端点，因此当前节点的$lmax$至少等于左儿子的$lmax$。

另外，若当前左儿子的$sum$加上右儿子的$lmax$更大的话，则更新$lmax$。

取左儿子的$sum$是保证一定包含左节点，取右儿子的$lmax$是保证连续性。

$rmax$同理转移。

image-20201212171931523

那么$mx$呢？

取$max{lson’s\ mx，rson’s \ mx，lson’s \ rmax + rson’s \ lmax} $即可。

取$lson’s \ rmax + rson’s \ lmax$的原因与上面相同，都是为了保证连续性。

最后，在$Query$函数中，由于需要维护左右儿子节点的各种参数，因此将返回值设为$SegmentTree$，每次返回对应节点线段树所维护的信息即可。

如果访问到了不需要的区间，为了避免对最终答案造成贡献，返回一个$mx,lmax,rmax$均为极小值的节点即可。

Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
#include <bits/stdc++.h>
#define maxn 4000005
#define lson(x) (x << 1)
#define rson(x) (x << 1) + 1
#define INF (1 << 30)
using namespace std;
int n, m, k, a[maxn];
struct SegTree{
    int lf;
    int rt;
    int val;
    int mx, lmax, rmax;
    SegTree() : lf(), rt(), val(), mx(), lmax(), rmax() {}
    SegTree(int lf, int rt, int val, int mx, int lmax, int rmax) : lf(lf), rt(rt), val(val), mx(mx), lmax(lmax), rmax(rmax) {}
} tree[maxn];
void Pushup(int now, SegTree t[]){
    t[now].val = t[lson(now)].val + t[rson(now)].val;
    t[now].lmax = max(t[lson(now)].lmax, t[lson(now)].val + t[rson(now)].lmax);
    t[now].rmax = max(t[rson(now)].rmax, t[rson(now)].val + t[lson(now)].rmax);
    t[now].mx = max(max(t[lson(now)].mx, t[rson(now)].mx), t[lson(now)].rmax + t[rson(now)].lmax);
}
void Build(int now, int lf, int rt, SegTree t[]){
    t[now].lf = lf;
    t[now].rt = rt;
    if (lf == rt)
    {
        t[now].val = t[now].lmax = t[now].rmax = t[now].mx = a[lf];
        return;
    }
    int mid = (lf + rt) / 2;
    Build(lson(now), lf, mid, t);
    Build(rson(now), mid + 1, rt, t);
    Pushup(now, t);
}
void Update(int now, int pos, int k, SegTree t[]){
    if (t[now].lf == pos && t[now].rt == pos)
    {
        t[now].val = t[now].lmax = t[now].rmax = t[now].mx = k;
        return;
    }
    if (t[now].rt < pos || t[now].lf > pos)
    {
        return;
    }
    Update(lson(now), pos, k, t);
    Update(rson(now), pos, k, t);
    Pushup(now, t);
}
SegTree Query(int now, int lf, int rt, SegTree t[]){
    if (lf <= t[now].lf && rt >= t[now].rt)
    {
        return t[now];
    }
    if (lf > t[now].rt || rt < t[now].lf)
    {
        return SegTree(lf, rt, 0, -INF, -INF, -INF);
    }
    SegTree res = SegTree(lf, rt, 0, -INF, -INF, -INF);
    SegTree tmpl = Query(lson(now), lf, rt, t);
    SegTree tmpr = Query(rson(now), lf, rt, t);
    res.val = tmpl.val + tmpr.val;
    res.lmax = max(tmpl.lmax, tmpl.val + tmpr.lmax);
    res.rmax = max(tmpr.rmax, tmpr.val + tmpl.rmax);
    res.mx = max(max(tmpl.mx, tmpr.mx), tmpl.rmax + tmpr.lmax);
    return res;
}
int main(void)
{
    scanf("%d %d", &n, &m);
    for (int i = 1; i <= n; i++)
        scanf("%d", &a[i]);
    Build(1, 1, n, tree);
    for (int i = 1; i <= m; i++)
    {
        scanf("%d", &k);
        if (k == 1)
        {
            int a, b;
            scanf("%d %d", &a, &b);
            if (a > b)
                swap(a, b);
            printf("%d\n", Query(1, a, b, tree).mx);
        }
        else
        {
            int p, s;
            scanf("%d %d", &p, &s);
            Update(1, p, s, tree);
        }
    }
    return 0;
}

🆗HDU1540

题意

给出一个初始均为$1$的数列，每次有两个操作：

①选择一个元素变为$0$

②询问包含位置$pos$的由连续的$1$组成的段的最大长度

考察

单点修改+最长连续子段

分析

这一题和上面那题差不多。

难点在于这个段必须全部由$1$构成，这就要求修改$Update$和$Pushup$的过程来帮助解决这道题目。

首先，考虑边界情况，当节点只有一个元素时：

$lmax=rmax=val = 1$

然后，考虑节点有多个元素的情况：

由于$lmax$一定要包含区间的左节点，当前节点的$lmax$至少为左儿子的$lmax$。

这一点与上一题的一样的。

但是什么情况下才能像上一题一样有左儿子的$sum$加右儿子的$lmax$？

容易知道若左儿子都为连续的$1$，则有$rt - lf + 1 == lmax \ or \ rmax$。

也就是说只要左儿子节点满足这个条件就可以进行转移了。

右儿子同理。

另外一个难点在于对询问的处理。

这次询问的是包含某一特定点的连续子段。

同样先考虑能够结束的边界情况：

①当节点满足$lf == rt$时：

此时若节点为$1$，则返回$1$，否则为$0$；

②当节点恰好处在左儿子的$rmax$范围内：

直接返回$rmax$+右儿子的$lmax$；

③当节点恰好处在右儿子的$lmax$范围内：

直接返回$lmax$+左儿子的$rmax$；

然后考虑不能结束的其他情况：

④只要不满足上面的三个条件，就为不能结束的其他情况。

这需要需要进一步递归求解。

虽然我们不能直接结束，但能够确定需要寻找的位置在左儿子还是在右儿子。

这便于进一步分解大问题为可以直接结束的小问题。

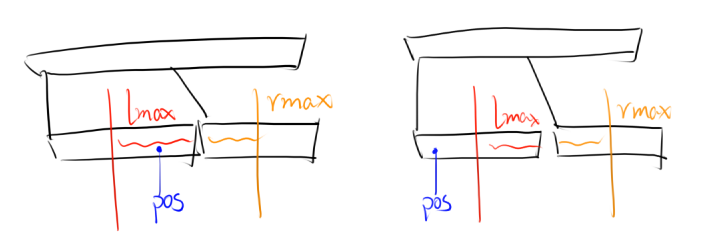
②③④情况如图所示：

image-20201212180258501

大概思路如上，剩下的就是代码实现了。

需要注意这题是多组数据，题面没说…

Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
#include <bits/stdc++.h>
#define maxn 400005
#define lson(x) (x << 1)
#define rson(x) (x << 1) + 1
#define INF (1 << 30)
using namespace std;
int n, m;
struct SegTree{
    int lf;
    int rt;
    int val;
    int lmax, rmax;
    SegTree() : lf(), rt(), val(), lmax(), rmax() {}
    SegTree(int lf, int rt, int val, int lmax, int rmax) : lf(lf), rt(rt), val(val), lmax(lmax), rmax(rmax) {}
} tree[maxn];
void Pushup(int now, SegTree t[]){
    t[now].val = t[lson(now)].val + t[rson(now)].val;

    t[now].lmax = t[lson(now)].lmax;
    if (t[lson(now)].rt - t[lson(now)].lf + 1 == t[lson(now)].lmax) 
        t[now].lmax = t[lson(now)].val + t[rson(now)].lmax;
    
    t[now].rmax = t[rson(now)].rmax;
    if (t[rson(now)].rt - t[rson(now)].lf + 1 == t[rson(now)].rmax) 
        t[now].rmax = t[rson(now)].val + t[lson(now)].rmax;
}
void Build(int now, int lf, int rt, SegTree t[]){
    t[now].lf = lf;
    t[now].rt = rt;
    if (lf == rt)
    {
        t[now].val = t[now].lmax = t[now].rmax = 1;
        return;
    }
    int mid = (lf + rt) / 2;
    Build(lson(now), lf, mid, t);
    Build(rson(now), mid + 1, rt, t);
    Pushup(now, t);
}
void Update(int now, int pos, int k, SegTree t[]){
    if (t[now].lf == pos && t[now].rt == pos)
    {
        t[now].lmax = t[now].rmax = k;
        return;
    }
    if (t[now].rt < pos || t[now].lf > pos)
    {
        return;
    }
    Update(lson(now), pos, k, t);
    Update(rson(now), pos, k, t);
    Pushup(now, t);
}
int Query(int now, int pos, SegTree t[]){
    if(t[now].lf == t[now].rt)
        return t[now].lmax + t[now].rmax;
    if (pos <= t[lson(now)].rt)
    {
        if(pos >= t[lson(now)].rt - t[lson(now)].rmax + 1)
            return t[lson(now)].rmax + t[rson(now)].lmax;
        else
            return Query(lson(now), pos, t);
    }
    else
    {
        if(pos <= t[rson(now)].lf + t[rson(now)].lmax - 1)
            return t[rson(now)].lmax + t[lson(now)].rmax;
        else
            return Query(rson(now), pos, t);
    }
}
char read(){
    char ch = getchar();
    while(ch != 'D' && ch != 'R' && ch != 'Q')  ch = getchar();
    return ch;
}
int main(void)
{
    while(~scanf("%d %d", &n, &m))
    {
        stack<int> s1;
        Build(1, 1, n, tree);
        for (int i = 1; i <= m; i++)
        {
            char ch = read();
            if (ch == 'D')
            {
                int p; scanf("%d", &p); s1.push(p);
                Update(1, p, 0, tree);
            }
            else if (ch == 'R')
            {
                int p = s1.top(); s1.pop();
                Update(1, p, 1, tree);
            }
            else 
            {
                int q; scanf("%d", &q);
                printf("%d\n", Query(1, q, tree));
            }
        }
    }
    return 0;
}
另解

考虑维护距离当前点的最近的被破坏的点。考虑维护两颗线段树，初始值均设为$0$。

然后，两颗线段树一颗维护最大值，一颗维护最小值。

每有村子被破坏时，将该点更新为对应的编号。

这样，设每次被破坏的点为$pos$，每次只需要在$[1, pos-1]$中寻找最大值，和在$[pos+1, n]$中寻找最小值，就是距离当前点最近的被破坏的点了。

结束

考前就写一下这些基本的先。

更多数据结构以后刷专题的时候再做一波。

啊，想起做线段树还不是因为上次ICPC复盘写炸了…