前言

一道不错的并查集题目，对于权值建图连边。最初模拟的时候队友一波就出来这个是并查集题，然后我跟着写了一发，可惜赛时$wa$了三个点。赛后发现，在合并的时候我的细节处理出了一些问题。

题意

传送门： B - Reversible Cards

给定$n$张牌，每张牌的正反面各有一个权值，为$a_i, b_i$，你可以随意翻转这些牌，使得最后这$n$张牌朝上展示的不同的数字数目最多。

思路

以样例展开：

$Input$

1
2
3
4
5
4
1 2
1 3
4 2
2 3

$Output$

1
4

最开始的时候，我想的是维护一个反悔操作，使得前面选中的牌尽可能的不同。

如下图：

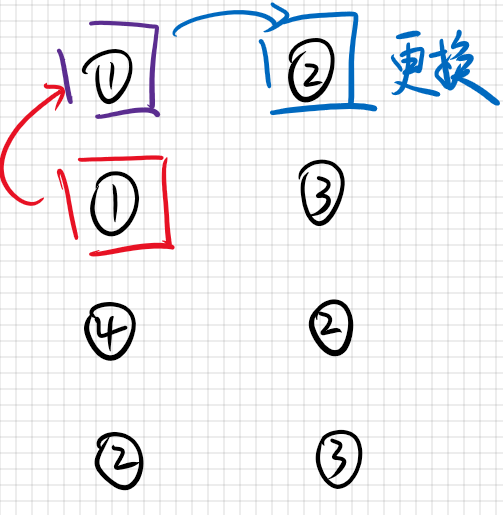
image-20210328170938806

  • 每一次贪心的选择第一个
  • 维护某个数字上一次出现的地方，如果出现相同的数字，就尝试修改该数字上一次出现的位置，如果能够更改就更改，如果不能更改，就考虑修改当前牌选择的数字。
  • 主要思想是保障前$i$个数不同个数最多

理论上是可以通过的，但是维护写起来比较麻烦，所以后面就没写下去了，写了队友的并查集想法。

如图所示：

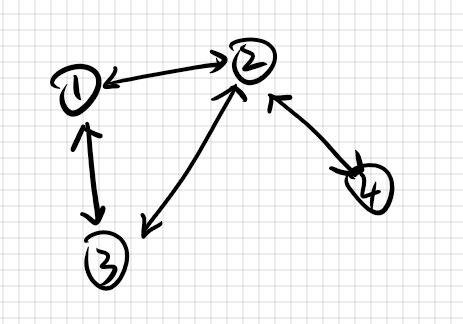
image-20210328171541281

把同一张牌两面的权值，当作点的编号，进行连边。

其实题目的数据范围也暗示了这一点，保证了权值范围在$4 * 10^5$内。（当然这也不绝对，某些时候可能需要使用$map$等重编号对应的点）

这样，选择不同权值的问题，就转化成了选择某条边连接的两点中某一个的问题。

我们容易发现，这样建出来的图，每一个连通块对答案的贡献是互不影响的。

也就是说，我们只要对每一个连通块求解就行。

设当前连通块的元素个数为$size$：

  • 当目前这个连通块内不存在环，重边时，或者说当前连通块是一颗树时，对答案的贡献为$size-1$；

  • 否则，每一个点都能够被选择到，对答案的贡献为$size$；

在实现的时候，我们可以使用并查集。

若当前连边的两个元素，有共同的祖先（已经在同一连通块内），则当前连通块存在环。

我这里选择使用一个$flag$数组进行标记连通块情况。

最后，在连接完所有边后，使用一个$map$，计算对应祖先下的连通块的元素个数。

得到每个连通块的大小后，就可以根据$flag$计算对应的贡献了。

这里开始的时候我写挂了一发，最初我的$flag$是只标记了合并时发现有环的集合。在一个不为树的集合合并到一个为树的集合时，flag数组不会更新，因此$wa$了三个点。

修改后交了一发就过了。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include <bits/stdc++.h>
#define maxn 800005
#define int long long
using namespace std;
int n, a, b, uset[maxn], flag[maxn], vis[maxn];
map<int, int> mp;
int find(int x){
    return x == uset[x] ? x : uset[x] = find(uset[x]);
}
void unioon(int x, int y){
    int fx = find(x);
    int fy = find(y);
    if(fx == fy)    
    {
        flag[fx] = 1;
        return;
    }
    uset[fx] = fy;
    flag[fx] = flag[fy] = (flag[fx] | flag[fy]);
}
signed main(void)
{
    //freopen("1_009.txt", "r", stdin);
    scanf("%lld", &n);
    for(int i = 1; i <= maxn - 5; i++)    uset[i] = i;
    for(int i = 1; i <= n; i++)
    {
        scanf("%lld %lld", &a, &b);
        unioon(a, b);
        vis[a] = vis[b] = 1;
    }  
    for(int i = 1; i <= maxn - 5; i++)
    {
        if(vis[i])
        {
            mp[find(i)]++;
        }
    }
    int ans = 0;
    for(map<int, int>::iterator iter = mp.begin(); iter != mp.end(); iter++)
    {
        if(flag[(*iter).first])
            ans += (*iter).second;
        else
            ans += (*iter).second - 1;
    }
    printf("%lld\n", ans);
    return 0;
}

别的

（没有思维的我是弟弟）