前言

前言鸽了

复盘

F - xay loves trees

如果知道怎么用Dfs序维护没有祖先关系或许就是模板题了，不过我是第一次做这种题目…

题意：给定两棵树，两棵树节点一一对应。要求在第一棵树上选择一条链，第二棵树上对应的点中任何两点没有祖先关系，问最多能够选择多少个点？

本题的关键是把没有祖先关系这一点对应到$dfs$​序上面。我们可以在$dfs$序上建立一颗线段树，然后当某个点加入被选择的集合中时，对以该点为根的子树的所有点的值$+1$（对$dfs$序，就是在一段连续的区间上进行一次区间加法）。

那么，只要整个区间的最大值为$1$​，就代表第二棵树上任意两点都没有祖先关系。

而后，对第一棵树，只需要$dfs$每一条可能的链，判断第二棵树上有无出现非法情况，并设置一个栈用于回滚区间加操作的影响，就能完成该题。

感觉这道题代码可以作为模板使用了，写的真不戳

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
/* vegetable1024 | liushan.site | Maybe Lovely? */

#include <bits/stdc++.h>
#define maxn 2000005
#define int long long
#define lson(x) (x << 1)
#define rson(x) (x << 1 | 1)
using namespace std;

//DEBUG TEMPLATE
template<typename T>
void Print(T value){
    std::cout << value << '\n';
}
template<typename Head, typename... Rail>
void Print(Head head, Rail... rail){
    std::cout << head << ", ";
    Print(rail...);
}

int read(){
    int x = 0; char ch = getchar();
    while(ch < '0' || ch > '9')    ch = getchar();
    while(ch >= '0' && ch <= '9')  x = x * 10 + ch - '0', ch = getchar();
    return x;
}

int t, n;
struct Graph{
    int k, head[maxn];
    struct Edge{
        int to;
        int nxt;
    } E[maxn];
    void inits(){
        k = 0;
        memset(head, -1, sizeof(head));
    }
    void Build(int u, int v){
        E[k].to = v;
        E[k].nxt = head[u];
        head[u] = k++;
    }
} g1, g2;

struct SegTree{
    struct Node{
        int lf, rt, mx, lazy;
    } tr[maxn];
    void Build(int now, int lf, int rt){
        tr[now].lf = lf;
        tr[now].rt = rt;
        if(lf == rt){
            tr[now].mx = 0;
            return;
        }
        int mid = (lf + rt) / 2;
        Build(lson(now), lf, mid);
        Build(rson(now), mid + 1, rt);
        tr[now].mx = max(tr[lson(now)].mx, tr[rson(now)].mx);
    }
    void Pushdown(int now){
        if(tr[now].lazy)
        {
            tr[lson(now)].mx += tr[now].lazy;
            tr[rson(now)].mx += tr[now].lazy;
            tr[lson(now)].lazy += tr[now].lazy;
            tr[rson(now)].lazy += tr[now].lazy;
            tr[now].lazy = 0;
        }
    }
    void Update(int now, int lf, int rt, int val){
        if(tr[now].lf >= lf && tr[now].rt <= rt){
            tr[now].mx += val;
            tr[now].lazy += val;
            return;
        }
        if(tr[now].lf > rt || tr[now].rt < lf){
            return;
        }
        Pushdown(now);
        Update(lson(now), lf, rt, val);
        Update(rson(now), lf, rt, val);
        tr[now].mx = max(tr[lson(now)].mx, tr[rson(now)].mx);
    }
} mxt;

int tp, bo, ans, stk[maxn];
int cnt, in[maxn], out[maxn];

void pre(){
    n = read();
    g1.inits(); g2.inits();
    for(int i = 1; i <= n - 1; i++)
    {
        int u = read(), v = read();
        g1.Build(u, v); g1.Build(v, u);
    }
    for(int i = 1; i <= n - 1; i++)
    {
        int u = read(), v = read();
        g2.Build(u, v); g2.Build(v, u);
    }
    tp = -1, bo = 0;
    ans = 0;
    cnt = 0;
    memset(mxt.tr, 0, sizeof(mxt.tr));
    mxt.Build(1, 1, n);
}
void dfs1(int now, int fa, const Graph &G){
    in[now] = ++cnt;
    for(int i = G.head[now]; ~i; i = G.E[i].nxt){
        if(G.E[i].to == fa)    continue;
        dfs1(G.E[i].to, now, G);
    }
    out[now] = cnt;
}
void dfs2(int now, int fa, const Graph &G){
    int flag = -1;
    stk[++tp] = now;
    mxt.Update(1, in[now], out[now], 1);
    if(mxt.tr[1].mx == 1){
        ans = max(ans, tp - bo + 1);
    }
    else if(tp - bo + 1 > ans){
        flag = stk[bo++];
        mxt.Update(1, in[flag], out[flag], -1);
    }
    for(int i = G.head[now]; ~i; i = G.E[i].nxt){
        if(G.E[i].to == fa)    continue;
        dfs2(G.E[i].to, now, G);
    }
    if(flag != -1){
        mxt.Update(1, in[flag], out[flag], 1);
        stk[--bo] = flag;
    }
    mxt.Update(1, in[now], out[now], -1);
    tp--;
}
signed main(void)
{
    t = read();
    while(t--)
    {
        pre();
        dfs1(1, 0, g2);
        dfs2(1, 0, g1);
        printf("%lld\n", ans);
    }
    return 0;
}

H - xay loves count

签到题。

设置一个桶统计每个数字出现的次数，然后枚举每个数以及它的倍数即可。

复杂度计算与调和级数相同，为$O(nlogn)$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
/* vegetable1024 | liushan.site | Maybe Lovely? */

#include <bits/stdc++.h>
#define maxn 2000005
#define int long long
using namespace std;

//DEBUG TEMPLATE
template<typename T>
void Print(T value){
    std::cout << value << '\n';
}
template<typename Head, typename... Rail>
void Print(Head head, Rail... rail){
    std::cout << head << ", ";
    Print(rail...);
}

int read(){
    int x = 0; char ch = getchar();
    while(ch < '0' || ch > '9')    ch = getchar();
    while(ch >= '0' && ch <= '9')  x = x * 10 + ch - '0', ch = getchar();
    return x;
}
int n, ans, a[maxn], b[maxn];
signed main(void)
{
    n = read();
    for(int i = 1; i <= n; i++)
        a[i] = read(), b[a[i]]++;
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= n / i; j++)
                ans += b[i] * b[j] * b[i * j];
    printf("%lld\n", ans);
    return 0;
}

I - xay loves or

签到题，考察细节…

主要是判断每一位取$1$和取$0$的可能性，并且要保证$1 \leq x < s \leq 2^{31}$​，也就是$s$不能全$0$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/* vegetable1024 | oi-liu.com | Maybe Lovely? */

#include <bits/stdc++.h>
#define maxn 65
#define int long long
using namespace std;
int x, s, c1, n1[maxn], c2, n2[maxn];
int read(){
    int x = 0; char ch = getchar();
    while(ch < '0' || ch > '9')    ch = getchar();
    while(ch >= '0' && ch <= '9')  x = x * 10 + ch - '0', ch = getchar();
    return x;
}

signed main(void)
{
    x = read();
    s = read();
    while(x)
        n1[++c1] = x & 1, x /= 2;
    while(s)
        n2[++c2] = s & 1, s /= 2;
    int flag = 0;
    for(int i = c1; i > c2; i--)
        if(n1[i])    flag = -1;
    int cnt = 0, sp = 1;
    for(int i = c2; i >= 1; i--)
    {
        if(n1[i] == 1 && n2[i] == 1)    cnt++;
        if(n1[i] == 1 && n2[i] == 0)    flag = -1;
        if(n1[i] == 0 && n2[i] == 1)    sp = 0;
    }
    if(flag == -1)
    {
        printf("0\n");
        return 0;
    }
    printf("%lld\n", (1LL << cnt) - sp);
    return 0;
}

J - xay loves Floyd

涨知识了，之前确实不知道这样写会出错，不过据说不论顺序，只要运行三次就都是对的（

第一次做跟$bitset$相关的题目，感觉这个优化真的狗（

首先由$n, m$判断，本题在$n$很大时是个经典的稀疏图，因此可以用$Dijkstra$，以每一个点为原点，建立正确的最短路关系，这一步复杂度为$O(nmlogm)$​​。

有了正确的最短路关系后，我们考虑按照题目的枚举顺序，要怎么样才能够获得正确的答案。

这里可以参考一下题解，讲的很清楚：

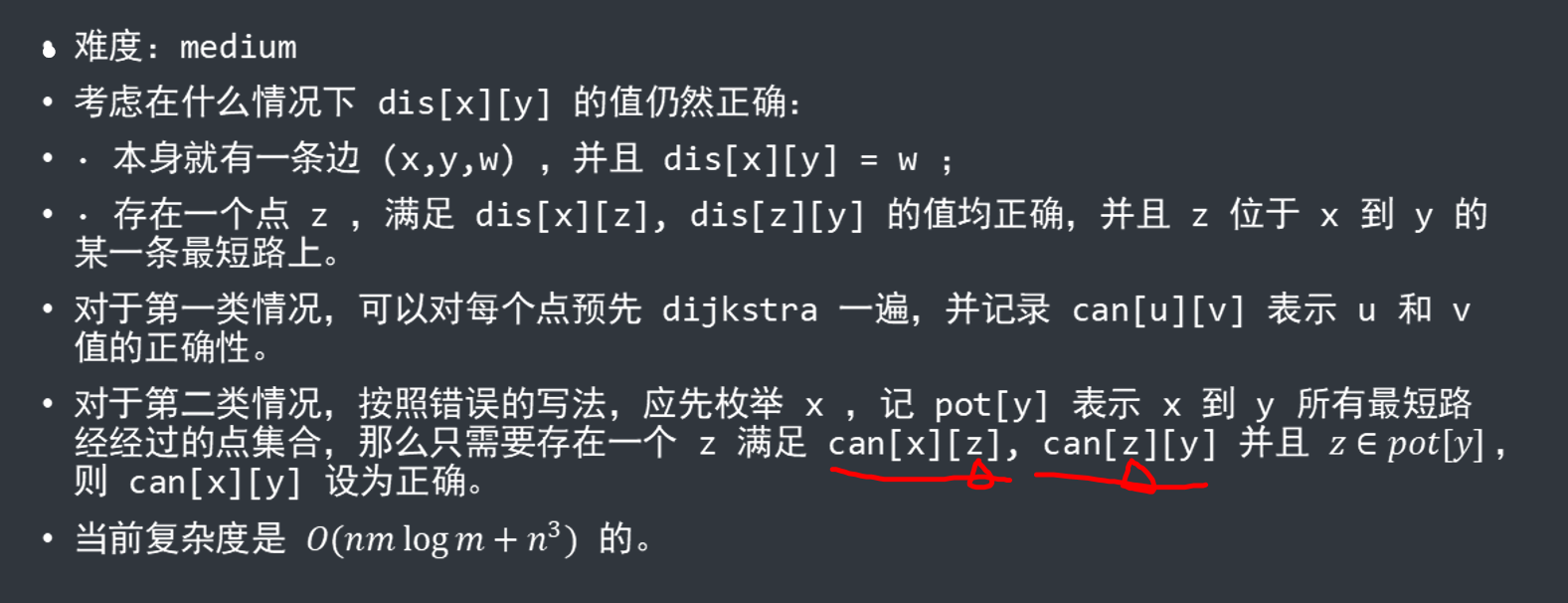
image-20210904171649939

但是$O(n^3)$的复杂度是难以通过这题的，我们需要更优秀的算法。

考虑$bitset$优化，对于$can[x][z], can[z][y]$，我们改写为$bitset\langle X \rangle f[x], g[y]$。

此时$f[x][i]=1 \leftrightarrow can[x][i] = 1$​，但是在计算的时候有了常数优化，一般为$/32$或者$/64$​。

最初的时候，我们对其赋初值$f[x][x]=1,g[y][y]=1$，代表自己到达自己是合法的。

而对于本身就存在一条边是最短的情况，同样赋值$f[u][v]=g[v][u]=1$，到此就可以开始模拟$Floyd$了。

首先我们枚举$s = 1\dots n$，此处$s$同$x$，为起点之意。

在枚举的过程中，为了进一步从$f[x][z],g[y][z]$推导到$f[x][y],g[y][x]$，需要再维护一个最短路所经过的点。

我们可以简单的按照距离排序（也可以按照拓扑序），维护一个$pot[i]$。

当$E[i].w + dis[s][now] = dis[s][E[i].to]$​时，就说明所有$s$到$now$的最短路上的点都可以到达$E[i].to$。

即有$pot[E[i].to] |= pot[now]$。

由此，就可以快速处理第二种情况，即枚举每一个$y$，判断$f[x],g[y],pot[y]$有无交集，有则说明该点得到的最短路距离是正确的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
/* vegetable1024 | liushan.site | Maybe Lovely? */
#include <bits/stdc++.h>
#define maxn 5005
#define int long long
using namespace std;

//DEBUG TEMPLATE
template<typename T>
void Print(T value){
    std::cout << value << '\n';
}
template<typename Head, typename... Rail>
void Print(Head head, Rail... rail){
    std::cout << head << ", ";
    Print(rail...);
}

int read(){
    int x = 0; char ch = getchar();
    while(ch < '0' || ch > '9')    ch = getchar();
    while(ch >= '0' && ch <= '9')  x = x * 10 + ch - '0', ch = getchar();
    return x;
}

int n, m, dis[maxn], cdis[maxn][maxn];
int k, head[3 * maxn];
struct Edge{
    int to;
    int nxt;
    int weight;
} E[maxn];
struct Node{
    int now;
    int dis;
};
bool operator < (const Node &A, const Node &B){
    return A.dis > B.dis;
}
void Build(int u, int v, int w){
    E[k].to = v;
    E[k].nxt = head[u];
    E[k].weight = w;
    head[u] = k++;
}
int id[maxn];
bitset<maxn> fr[maxn], to[maxn], pot[maxn];
void Dijkstra(int x){
    priority_queue<Node> q1;
    memset(dis, 0x3f, sizeof(dis)); dis[x] = 0;
    q1.push((Node){x, 0});
    while(!q1.empty())
    {
        Node tmp = q1.top(); q1.pop();
        int now = tmp.now, dist = tmp.dis;
        if(dist != dis[now])    continue;
        for(int i = head[now]; ~i; i = E[i].nxt)
        {
            if(dis[E[i].to] > dis[now] + E[i].weight)
            {
                dis[E[i].to] = dis[now] + E[i].weight;
                q1.push((Node){E[i].to, dis[E[i].to]});
            }
        }
    }
    for(int i = 1; i <= n; i++)    cdis[x][i] = dis[i]; 
    for(int i = head[x]; ~i; i = E[i].nxt)
        if(E[i].weight == cdis[x][E[i].to])
            fr[x][E[i].to] = to[E[i].to][x] = 1;
}
int solve(int s){
    for(int i = 1; i <= n; i++){
        pot[i].reset();
        pot[i].set(i);
    }
    for(int i = 1; i <= n; i++)    id[i] = i;
    sort(id + 1, id + n + 1, [&](const int &A, const int &B){return cdis[s][A] < cdis[s][B];});
    for(int i = 1; i <= n; i++)
    {
        int now = id[i];
        for(int j = head[now]; ~j; j = E[j].nxt)
            if(cdis[s][now] + E[j].weight == cdis[s][E[j].to])
                pot[E[j].to] |= pot[now];
    }
    for(int i = 1; i <= n; i++) 
        if(cdis[s][i] > 1e9 || (pot[i] & fr[s] & to[i]).count())
            fr[s][i] = to[i][s] = 1;
    return fr[s].count();
}
signed main(void)
{
    memset(head, -1, sizeof(head));
    n = read(); m = read();
    for(int i = 1; i <= m; i++)
    {
        int u, v, w;
        u = read(); v = read(); w = read();
        Build(u, v, w);
    }
    for(int i = 1; i <= n; i++)
        fr[i].reset(), fr[i][i] = 1, to[i].reset(), to[i][i] = 1;
    for(int i = 1; i <= n; i++)    Dijkstra(i);
    int ans = 0;
    for(int i = 1; i <= n; i++)    ans += solve(i);
    printf("%lld\n", ans);
    return 0;
}

题解中还提到另一种更优秀的做法：

image-20210904173527290