前言

这牛客$4,5$怎么都变成自闭场了，补题选手极度不友好（雾）

第$6$场就很简单，居然还出来一些很简单的模板题…不过$4,5$是真的难顶…

这一题的话，一个是排列组合怎么解很不错，另一个是控制变量打表的写法，记录一下…

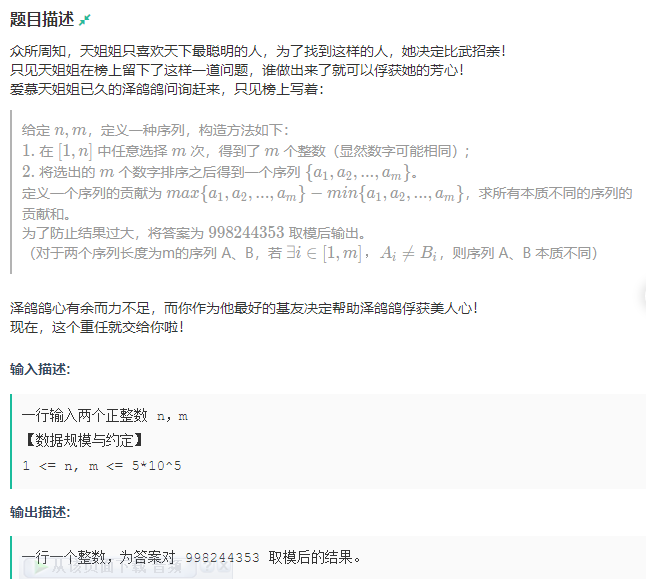
题目

---

解法

第一次做的时候并没有往枚举$max - min$的方向去想，然后自闭了。

首先，我们可以容易发现，假设$max-min=x$，$x$相同的所有序列，提供的贡献是一样的。

比如$min=1,max=6$，和$min=10,max=15$，所提供的贡献值是相同的。

然后，我们就可以枚举$x$，得到最终的贡献值：

$$ans=\sum_{i=0}^{n-1} (n-i) * i * calc(i) \quad (Mod \ M)$$

其中，$calc(i)$是计算当前差值下，且$min$和$max$确定时，能够提供的本质不同的序列个数。$i$为当前每一种序列都能提供的贡献值，$(n-i)$为能提供的确定$min$和$max$的对数。

考虑计算$calc(i)$，我们假定$min=a,max=b$，有下图：

---

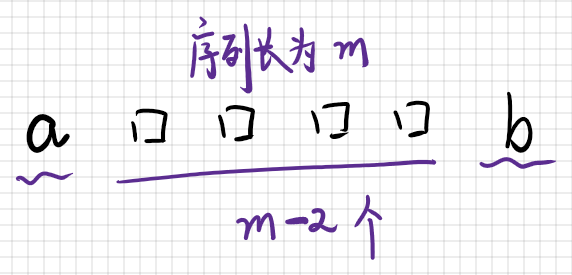
这个序列是排序之后的，因此，我们可以设整个序列应该是单调不减的。

此时，我们考虑使用一种方法表示这种性质。

我们可以在这$m$个数的空隙间插板，每一块插板比作$+1$，如下图所示：

---

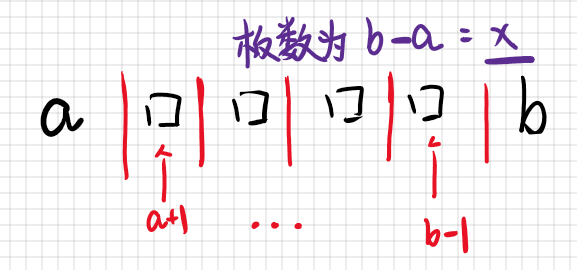
这是一种特殊的插板方式，每一空隙都最多插入一个插板，此时方案数为$C_{m-1}^{x}$。

但是在这一题里面，每一空隙是可以插入多个隔板的，就像：

---

所以我们考虑绑定隔板和空隙，在插入一个隔板时同时，在隔板左边提供一个新的空隙，便于新的隔板插入。

为获得更直观的例子，设$min=2,max=7$，如图所示：

---

此时，方案数为$C_{m+x-2}^{x}$。

在插入$x$个板子之后，空位个数为$m+x-1$，但最左边的空位不能使用，因此得到$m+x-2$。

只要按照这个流程，枚举每一种差值即可。

另一解释

给好队友推了这一题，队友找了一种类似的小球模型的解释给我，感觉很不错！

---

打表出奇迹

如果实在推不出，就要考虑能不能找到对应的规律了。

下图来自@Kur1su的题解：

---

别的

最近还是有点鸽啊，没有补多少题，补完还得去练习$Codeforce$…

加油吧φ(*￣0￣)